無偏差最小二乘法伺服控制系統參數辨識
2018-4-18 來源:合肥工業大學 作者:吳路路 韓江 田曉青 夏鏈
摘要:為準確辨識伺服控制系統參數,針對高性能運動控制算法的要求,在分析典型伺服控制系統結構模型基礎上,基于“庫侖摩擦+黏性摩擦”模型,設計了無偏差最小二乘方法,研究其在“工控機+運動控制卡”數控系統平臺上的實現方法。實時采集電機角速度數據,利用設計的方法估算伺服系統轉動慣量、黏性摩擦和庫侖轉矩,通過角速度重構,對比理論計算和實際測量角速度,驗證參數辨識的有效性和準確性。理論分析和實驗結果表明,所設計的參數辨識方法能夠準確辨識系統參數。
關鍵詞:伺服控制;無偏差最小二乘法;角速度重構;參數辨識
0、引言
設計高性能的伺服驅動控制系統,需要準確辨識執行機構的動力學參數。起初,控制系統都是基于偏差調節的反饋控制方式,為了降低運動軌跡的輪廓誤差,要求各運動軸有匹配的閉環動態響應。隨后,在傳統反饋控制器的基礎上,人們又提出前饋控制算法,即在控制器中引入了預估前饋數據。Tomizuka提出了一種零相位誤差前饋控制器(ZPETC),通過在前饋控制器中輸入零點來補償閉環系統的不穩定零點,增加控制系統的帶寬,提高伺服系統的跟蹤精度。然而,對于ZPETC控制算法而言,如果想要設計具有較強魯棒性的控制器,需要準確獲取反饋系統的模型參數。
Ramesh等指出,如果控制系統參數與實際控制對象的參數不匹配,則使用前饋控制器反而會降低系統的控制精度,即使采用最小方差(generalised minimum variance)和極點配置方法設計系統控制器,如果想獲得較好的控制性能也需精確知曉控制對象的參數。從工業上廣泛使用的 P、PI、PID 控制器,到較為復雜的 ZPETC 控制器,再到更復雜的集成控制器,雖然各種控制算法都有一定的抗干擾能力,但對于突變的干擾來說,這些控制算法都需要一定的時間來消除突變干擾的影響。在圓弧插補的過象限處和線性輪廓拐角處,運動軸方向改變,摩擦力方向會隨之發生突變,由于無法及時消除摩擦力的影響,該位置的精度會顯著降低。解決這一問題的方式就是利用已知的信息(如插補的參考位置、速度),提前預估即將產生的干擾情況,通過前饋補償的方式來消除突變干擾對系統運動精度的影響。然而,對于這種提前補償的方式,需要預先獲取突變干擾的特征。就進給系統中因運動方向改變而發生突變的摩擦干擾而言,需要提前掌握摩擦的特征才能進行補償。
本文通過最小二乘法辨識進給驅動系統的動力學模型參數和摩擦干擾的特征參數,進給系統模型采用典型模 型,摩擦干 擾 模型采用 “庫侖摩擦+黏性摩擦”模型。模型辨識實驗在基于“工控機+運動控制卡+伺服電機”的運動控制平臺上實現,通過重構電機運行速度,驗證模型辨識的有效性。
1、伺服控制系統建模
伺服控制系統模型采用在實際應用中廣泛使用的慣量阻尼模型,摩擦模型則采用“庫侖摩擦+黏性摩擦”的結構。摩擦是影響進給系統控制精度的主要干擾因素,因此本文主要考慮摩擦因素,忽略測量噪聲、量化誤差等次要因素對模型參數的影響。
1.1 伺服系統模型
圖1所示的進給驅動系統模型在伺服控制系統中廣泛使用,系統中等效轉動慣量為、黏性摩擦因數為B。u是輸入的電壓控制信號,由于伺服驅動系統的電流環帶寬在幾千赫茲以上,遠高于系統的采樣頻率,因此電流環可簡化成一個比例放大環節,比例系數為 Ka。經過驅動器的放大作用,在電機電樞中產生電流i,電機轉動形成驅動轉矩 Tm,電機的轉矩常數為 Kt。 除了電機產生的驅動轉矩 Tm外,導軌、絲杠、軸承上的摩擦力會在電機軸上產生干擾轉 矩 Tf,驅 動 轉 矩Tm 和干擾轉矩Tf共同作用驅動電機軸轉動。轉動角速度為ω,電機軸連接導程為rg的滾珠絲杠副,經由絲杠將角速度轉化為伺服系統的直線運動速度,直線運動速度為x·,經過一個積分環節得到伺服軸的位置x。
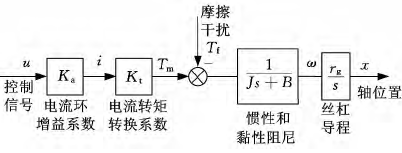
圖1 伺服控制系統模型


1.2 摩擦模型
文獻中對各種摩擦模型做了詳細的闡述,“庫侖摩擦 + 黏性摩擦”模型能夠較準確地反映摩擦特性,相比其他摩擦模型而言結構簡單,用較少的參數體現摩擦的特征,在工程中得到較廣泛的使用。
文獻從工程實用角度采用圖2所示的模型,很好地補償了摩擦的影響,摩擦轉矩Tf與軸轉速ω在一定程度上成線性關系。
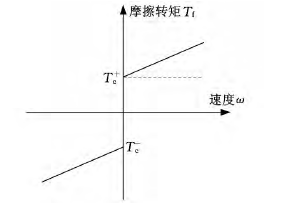
圖2 摩擦模型
當驅動轉矩小于庫侖摩擦轉矩Tc時,伺服系統運動軸處于停止狀態,當軸運動后,隨著角速度值增加,摩擦轉矩成現線性比例增長,直線的斜率為進給驅動系統的黏性摩擦因數 B,當運動方向發生改變時摩擦轉矩發生突變。摩擦轉矩與角速度的關系如下公式所示:

2、系統參數辨識
利用圖1所示的伺服系統模型和圖2所示的摩擦模型,在一個簡化的伺服系統上進行參數辨識實驗。系統辨識采用兩種方式:簡單最小二乘法和無偏差最小二乘法。簡單最小二乘法忽略庫侖摩擦的影響,默認 Tc=0,實際辨識過程中只需估算轉動慣量和黏性摩擦因數值;無偏差最小二乘法考慮摩擦干擾的影響,需要估算慣量、黏性摩擦因數和庫侖摩擦值。
2.1 簡單最小二乘法系統參數辨識
采用簡單最小二乘法忽略運動方向改變時的摩擦突變的影響,認為 Tc=0。
根據式(3),如果

2.2 無偏差最小二乘法系統參數辨識
在實際工作過程中,由于干擾的存在可能會使得估算值出現較大偏差,故需要考慮干擾對估算值的影響,此時式(3)寫成如下形式:

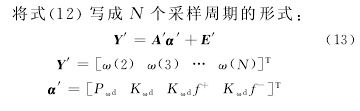

3、參數辨識實驗
通過兩種方法辨識伺服控制系統的轉動慣量和黏性阻尼系數,與平臺的實際轉動慣量對比,驗證無偏差方法的準確性;然后將兩種方法辨識的結果分別代入到伺服系統模型中,根據輸入指令計算系統的理論輸出速度,并分別與實際采集的速度作對比,分析兩種方法的速度偏差,驗證無偏差方法的有效性。
3.1 實驗平臺
伺服系統參數辨識實驗是在基于“工控機+運動控制卡+伺服電機”的平臺上進行的,如圖3所示。工控機通過以太網總線向運動控制卡發送控制指令,運動控制卡根據指令值控制電機運轉,實時采集電機編碼器反饋的脈沖值,根據反饋值計算電機實際轉動的角速度;將電機的實際角速度實時反饋給工控機,工控機將對應時刻的角速度值寫入相關文檔,用于相關參數辨識。

圖3 實驗平臺結構


3.2 參數辨識
實驗輸入的指令是一系列階躍電壓信號,指令電壓先增大再減小,共進行3組實驗,如圖4所示。3組實驗中,指令電壓值從0增加到每組實驗的最大值,再減小到0,相應階躍點的控制電壓值如表1所示,3組實驗的最大值分別為75mV、100mV 和150mV,最小值為0。
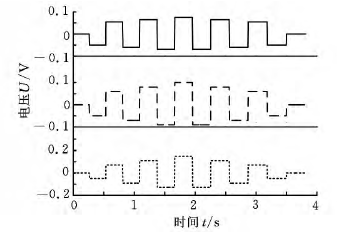
圖4 3組實驗指令電壓信號
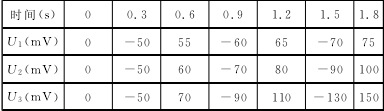
表1 指令電壓值
利用 PMAC 運動控制卡實時采集電機的速度值,利用式(7)和式(14)分別對系統的參數進行估算,得到轉動慣量、黏性摩擦和庫侖摩擦轉矩的估計值。表2是通過簡單二乘法獲得的轉動慣量和黏性摩擦值。表3是通過無偏差最小二乘法得到的轉動慣量、黏性摩擦值和庫侖摩擦轉矩值。圖5是3組實驗的估算值對比圖。
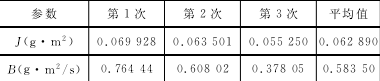
表2 簡單最小二乘法估算值
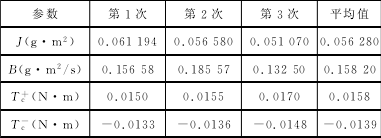
表3 無偏差最小二乘法估算值
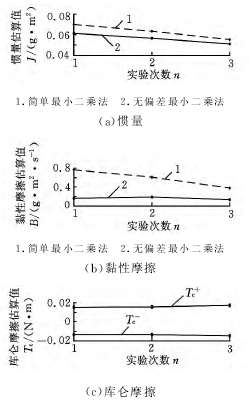
圖5 實驗數據對比
對比3組實驗的估算值,簡單最小二乘法得到的轉動慣量和黏性摩擦值相對較大,且3組實驗結果存在較大差異,無偏差最小二乘法3組實驗得到的估算值波動較小,三次實驗的結果基本一致。由表2可得簡單最小二乘法3組實驗的平均估算值為

對比實際和辨識所得的伺服控制平臺的轉動慣量值,從以上的估算結果可以看出,兩種方式估算得到的轉動慣量值都很接近實際值,兩種方式都能很好地辨識系統的轉動慣量。然而,簡單最小二乘方式辨識得到的轉動慣量和黏性摩擦的值相對無偏差方式較大,而且3次辨識的結果差別較大。簡單最小二乘法未考慮庫侖摩擦的影響,將庫侖摩擦的影響轉化成黏性摩擦的影響,致使黏性摩擦和轉動慣量 值增大并使得結果波動較大。
為了驗證辨識參數的有效性和準確性,將辨識獲得的參數代入到理論模型中,根據輸入的電壓指令計算并重構理論角速度,將理論角速度與實測角速度相比較,結果如圖6所示。
采用簡單最小二乘方式重構的角速度最大誤差值為15rad/s,無偏差方式重構的角速度誤差值為7rad/s,不到前一種方式 的一 半,采 用 無 偏 差 方式辨識獲得的參數重新構建的角速度與實際的角速度相符度更高,更能準確地描述實際伺服系統。
采用無偏差方式估算的參數計算得到的理論角速度曲線更接近實測角速度曲線,而且角速度誤差波動更小。
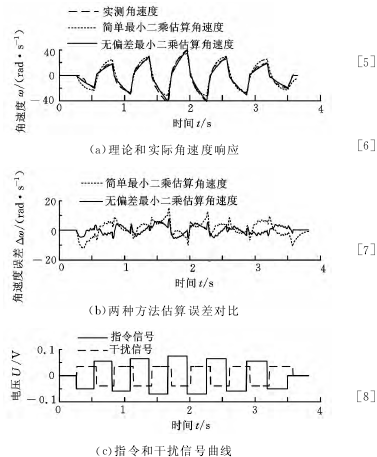
圖6 角速度重構與分析圖
4、結語
本文分析了伺服控制系統結構模型,采用無偏差最小二乘方法,基于“庫侖摩擦+黏性摩擦”模型,辨識伺服控制系統參數。研究了最小二乘法參數辨識在“工控機+運動控制卡”數控平臺上的實現方法,從理論和實驗的角度分析了辨識方法的準確性。通過辨識實驗獲得系統的參數,并將估算得到的系統參數代入系統模型,重構電機角速度。實驗結果表明,所采用無偏差最小二乘方法可以更準確地辨識系統的參數。
投稿箱:
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
更多相關信息




