基于遺傳算法的雙機器人加工中心布局優化
2016-8-18 來源:南京理X-大學 作者:王軍 曹春平 丁武學 孫宇
摘要:首先建立了面向大型儀表板的雙機器人作業加工單元,為了保證機器人和工件不發生碰撞,提出了以雙機器人的工作空間重合率最大為目標、基于遺傳算法的雙機器人加工中心優化布局方法,建立了空間約束的數學模型,利用MATLAB軟件進行仿真分析,并從空間重合率、加工周期兩個方面進行比較。結果表明:相對于公司現有狀態,空間重合率提高了14.6%,加工周期縮短了1.2 min,驗證了該方法的有效性和可行性。
關鍵詞:機器人;加工中心;布局優化;遺傳算法
0 、引言
近年來,機器人在工業領域已經被廣泛應用,如焊接、鉆孔、裝配、運輸、噴涂等,尤其是在汽車制造領域。在汽車內飾領域,儀表板屬多型號小批量生產,不同型號儀表板上孔的位置、形狀、大小分布都不同,甚至差距很大。越來越多的企業引進多機器人加工單元進行汽車儀表板的加工,以期在保證加工精度的前提下提高工作效率,縮短工作周期。多機器人加工中心布局優化問題一直是國內外學者關注的重點。
在多機器人布局優化領域,Chedmail等[11通過修改機器人模型的D—H參數,并用八又樹表示機器人機器人工作空間和目標空間,同時引入避碰檢測來確定加工中心的布局;Kats[2。利用優化算法來求解所有無碰撞路徑的最小值,并以此為依據進行布局設計;Chittajallu等[31用圓形外包的方式描述布局設備,這種簡化方式便于設備之間的干涉檢驗,但布局空間不能得到合理有效的利用;Barral等H3提出了基于模擬退火算法的布局方法,并在工業機器人軟件平臺IGRIP上運用,由于模擬退火算法本身的特性使得計算時間較長,布局方案計算耗時較長;王召莉口3研究了機器人關節空間和操作空間的特性,將機器人的關節軌跡距離作為評估指標,采用簡單、高效的自適應差分進化算法對典型機器人作業單元的布局優化實例進行研究。
本文以某企業典型的汽車儀表板為加工對象,研究面向大型儀表板的雙機器人加工中心的布局優化問題。目標為在考慮兩個機器人和儀表板之間的位置關系基礎上保證機器人和工件不發生碰撞的前提下,使兩個機器人的工作空間重合率最大。通過對機器人、工件進行數學建模,并引入相關約束條件,利用遺傳算法對雙機器人加工中心的布局進行優化,最后采用MATLAB軟件¨1進行仿真分析,并從空間重合率、加工周期兩個方面進行比較。
1、問題描述與建模
1.1 問題描述
1.1.1儀表板的特點
汽車儀表板具有體積大、形狀復雜等特點,一般需要在銑削中心上完成多個孑L的加工。如圖1所示,儀表板上孔的位置、形狀、大小分布都不同,甚至差距很大。此外,儀表板兩側孔的數量不同,一側孑L多一側孑L少,且在加工過程中對象不能移動。若采用單個機器人加工則工作空間有限,不能獨自完成所有的任務,因此,需要至少兩個以上的機器人協調完成所有加工任務。

圖1某型號儀表板
1.1.2加工中心的配置
根據汽車儀表板的加工特點,初步布置了雙機器人加工中心。兩個機器人分布在儀表板的兩側,通過電機帶動機器人在導軌上左右移動,完成儀表板上所有工藝孔的加工,如圖2所示。
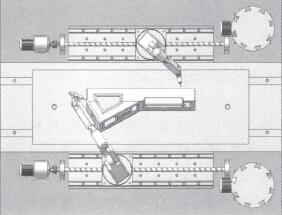
圖2 銑削加工中心布置示意圖
1.1.3方案設計
在機器人布局設計中,在給定機器人型號、尺寸的前提下,通過合理布局機器人和儀表板的位置關系,提高兩個機器人的空間重合率,使孔較少一側的機器人在加工完本側的孑L后,能夠加工少量對面的少量孔,從而提高加工效率,以達到縮短生產周期的目的[7]。
1.2建模
1.2.1機器人建棋
一般來說,機器人前三個自由度可以使機器人的末端執行器到達其工作空間內指定的任意位置,因此,可以只考慮擁有前三個自由度的操作臂,至于末端姿態可以在工件外給定一個容許空間,用剩余三個自由度來調整。單個機器人的模型簡圖見圖3。
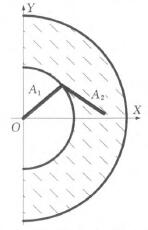
圖3單個機器人結構模型簡化圖
如圖4所示,當機械臂從點1運動到點2時,機械臂1一定會與工件發生碰撞,所以工件不能出現在半徑為A。的半圓內,因此,機械臂有效工作空間為圖3所示的陰影部分,數學模型為R一{(z,y)l A;≤z2+Y2≤(Al+A2)2,z≥0} (1)
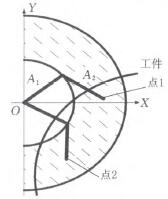
圖4 機械臂與工件一定會發生碰撞的情況
1.2.2 工件建模
將儀表板向其橫截面上投影,如圖5所示,加工對象所在的空間范圍簡稱為目標空間,是由兩個半徑不同的扇形圍成的區域。
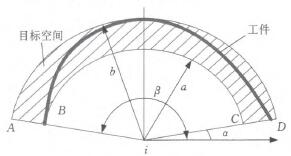
圖5 用扇形區域表示工件
目標空間在極坐標系中表示為W一{(驢,10)l a≤妒≤盧,a≤P≤b/ (2)式中,a、b分別為兩個圓弧的半徑;a、|9分別為目標空間在極坐標系中角度的極值。
因為在進行孔銑削時機器人末端執行器必須垂直于工件表面,所以需要給定一容許空間讓機器人調整末端姿態。因此,實際目標空間應當向外擴展一定距離,故目標空間中兩個圓弧的半徑分別為a+△L和b+AL。
1.2.3 約束模型
要求兩個機器人同時對儀表板進行孔加工,加工中必須滿足兩個基本原則:①工件必須完全在兩個機器人的工作空間內;②必須提供足夠的空間,讓兩個機器人避免碰撞。
為了滿足上述兩個原則,建立三個坐標系:兩個機器人直角坐標系和一個工件極坐標系,通過三個坐標系建立兩個機器人和工件之間的相對位置關系,如圖6所示,目標坐標系原點在兩個機器人的直角坐標系中的坐標分別為(z,了)和(“,口),驢。和驢:為描述機器人加工范圍的角度值,其中儀表板在坐標系1一側孔較多,在坐標系2一側孔較少。
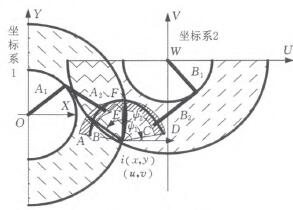
圖6 約束描述

(1)約束一:目標空間必須在機器人工作空間內。
要滿足約束一,點A、B必須在機器人1的加工范圍內,點C、D必須在機器人2的加工范圍內,即

同時,孔多一側的機器人1可以加工所有本側的孔,則點E、F必須在機器人1的加工范圍內;孔少一側的機器人2有能力加工對側的孔,則點E、F必須在機器人2的加工范圍內。即
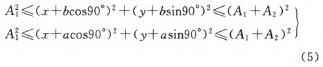
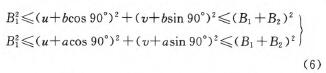
(2)約束二:A點不應該在機器人2的工作空間內部。一是為避免空間浪費,二是會造成兩個機器人距離太近,容易發生碰撞現象。

(3)約束三:為防止機器人在姿態調整過程中與工件發生圖4所示的碰撞,工件的任一部分都不能出現在以A,為半徑的圓弧內,故應滿足如下條件:
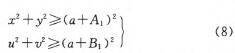
(4)約束四:兩機器人之間必須有足夠的空間,以便兩個機器人的安裝、維修以及避碰等,即
其中,d需要設計者根據實際情況給出。
1.2.4 目標函數
優化目標是在不發生碰撞的前提下,目標空間中兩個機器人的空間重合率盡量大。即
2、布局優化算法
上述過程將雙機器人加工中心的布局問題轉變成非線性規劃問題。傳統的非線性規劃算法的缺陷是計算煩瑣且精度不高,穩定性差,對函數初值和函數性態要求較高,且容易陷入局部最優解。而遺傳算法是一種全局搜索算法,可以克服傳統的非線性規劃算法容易陷入局部最優解的缺陷。因此,將遺傳算法應用于雙機器人布局優化問題以改善收斂效果,提高優化質量。
利用遺傳算法進行布局優化的步驟凹1如下:
(1)編碼。遺傳算法的編碼形式主要有二進制編碼和實數編碼,此處采用實數編碼。個體長度為6,4個描述位置關系的坐標值,2個描述機器人加工范圍的角度值。
(2)生成初始群體。利用constraintdependen創建函數隨機地生成N一100個初始個體,每個個體組合在一起形成一個群體,遺傳算法以這個群體作為初始種群進行迭代操作。
(3)適應度函數的確定。本文通過遺傳算法求解兩個機器人的最大空間重合率,相當于式
(10)所示的目標函數。因MATLAB遺傳算法工具箱要求目標函數為求最小值,且最小值需為正值,因此調整適應度函數為
繼而利用工具箱提供的適應度的尺度變換函數排列(rank)來確定最終的適應度函數,以此為標準評價個體解的好壞來引導搜索,使適應度函數最小化。
(4)選擇操作。本文采用輪盤賭選擇法(rou—lette函數)實現,假定個體i的適應度值為.廠:,則其被選擇的概率P,為

(5)交叉操作。由于個體采用了實數編碼方式,所以交叉操作也采用實數交叉法,這里采用基于實數編碼的交叉算子為算數交叉(ArithmeticCrossover)。假設兩個個體XA、X。之間進行算數交叉,則交叉后產生所產生的新個體為

(6)變異操作。因為上文采用的是實數編碼方式,此處采用均勻變異算子(uniform)進行變異操作。假設一個體為x一(X。,X。,X。,X。,X。,X。),X。為其中要變異的基因,則變異操作如下:

(7)循環。重復步驟(2)至步驟(6)直到滿足終止條件。
(8)以最好的染色體作為最優解。
3、實例和結果分析
3.1 仿真實例優化布局結果
以圖1所示型號儀表板為加工對象,并取廠內某型號的兩個機器人做實例分析,可得到兩個機器人的機械臂尺寸及工件模型的相關參數。
(1)已知條件。機械臂1的長度:A,一682 mm;A2—732 mm;機械臂2的長度:B1—1023 mm;B2—1145 mm;工件模型:a=987 mm;b一765;d一10。;盧一170。。
(2)6個變量。極坐標系原點在兩個直角坐標系里的坐標:(z,y)和(“,口)。描述機器人加工范圍的角度值:驢。,≯:。
通過遺傳算法進行優化求解,優化后的布局結果見表1。
表1 布局優化結果
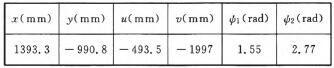
根據表1的優化結果,可得到極坐標系原點在兩個機器人坐標系中的坐標值,從而確定了兩個機器人和工件的一個較優的位置關系:

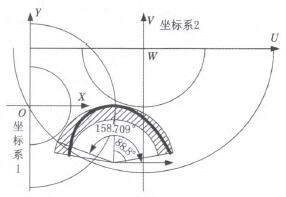
圖7 買際布局
3.2 仿真結果分析
根據仿真結果,對兩機器人進行重新布局后,從機器人工作的重合空間和加工周期兩個角度進行分析,驗證了算法的有效性。
3.2.1 重合空間大小的比較
由布局優化結果得出兩機器人的加工范圍f圖8)及幣合空間的大小:
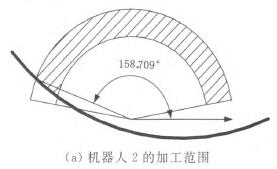
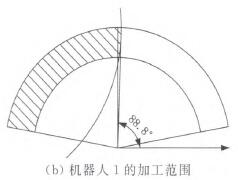
圖8 機器人的加工范圍
重合空間最大即驢z一≯,一69.9。。與實際機器人加工中心作比較,結果見表2。
表2 重合空間的比
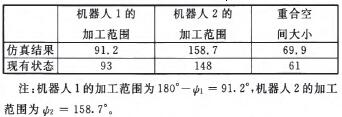
可以看出,在兩個機器人能完成各自任務的前提下,仿真結果表明此方法可以顯著提高兩個機器人的空間重合率。
3.2.2 加工周期的比較
(1)以圖1所示型號儀表板為對象,以兩個機器人加工時間相等為目標進行機器人加工任務的分配‘9|,如圖9所示。
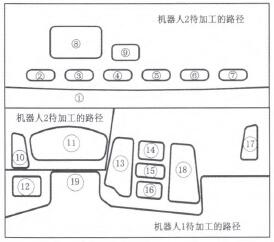
圖9 任務分配的結果
(2)在任務分配的基礎上,以兩個機器人的運動路徑最短為原則確定銑削加工順序。該問題是典型的TSP問題,因此采用蟻群算法‘101來實現路徑優化仿真,得到的優化路徑如圖10所示。
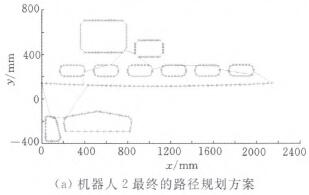
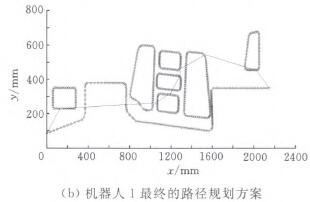
圖10 兩個機器人的路徑規劃方案
基于MATLAB平臺利用Robotics Toolbox工具箱實現對工業機器人的系統仿真。為方便數據統計及實現自動輸出,設計機器人加工中心控制器,如圖11所示。根據上述路徑規劃結果以及時間最優軌跡規劃,仿真得出機器人加工中心在加工過程中的總時間,并與現有的加工周期進行對比。

圖11 仿真控制器
仿真后得到單個儀表板的加工時間t。與工廠實際加工周期t。作比較,結果見表3。
表3加工周期的比較
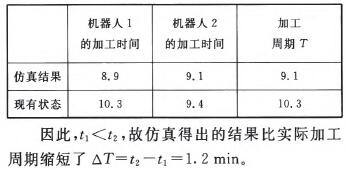
4、結語
本文通過對雙機器人加工中心建立數學模型,引入相關約束。結果表明,該數學模型可以準確描述兩個機器人和儀表板之間的位置關系,為后續的仿真及布局奠定基礎。
遺傳算法是一種全局搜索算法,可以有效解決傳統非線性算法容易陷入局部最優解的問題,成功求解雙機器人加工中心的最佳布局。
從仿真結果可以看出,通過該數學模型和遺傳算法的有效結合,可以顯著提高兩個機器人的空間重合率,為后續進行加工中心的任務分配及路徑規劃提供較大的靈活性,從而達到最小化加工周期的目標。
投稿箱:
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com





