0 前言
五軸加工在三軸加工基礎上增加了兩個旋轉軸,從而使加工方式更加靈活,材料去除率更高,加工時間更短,可以處理更為復雜的工件[1-2]。但是旋轉軸的運動也使刀具姿態控制更為復雜,從而引入許多五軸加工所特有的問題[3-4]。奇異點問題就是其中重要的一個。當刀具通過奇異點附近區域(本文稱奇異區域)時,旋轉軸會產生不連續并且急速的轉動,這大大增加了非線性誤差,同時極易破壞工件,甚至損傷機床部件[5-6]。因此,對奇異區域內的刀具路徑進行優化處理,對于提高加工精度和加工效率至關重要。
AFFOUARD 等[6]提出通過多項式插補修改刀具路徑來避開奇異位置,但是插補算法復雜,計算上代價較大。MUNLIN 等[7-8]通過選擇奇異點附近旋轉軸運動的最短路徑來減小誤差,但該方法在選擇轉角取值時,考慮的是相鄰點轉角變化量的相對值最小,而相鄰點之間轉角變化量的絕對值可能較大,出現這樣的情況時誤差仍然較大。SORBY[9]提出的方法是在奇異點附近插入刀位點,同時修改C軸轉角,避免加工通過奇異點時誤差過大,但由于之前沒有對奇異區域的范圍進行檢測,因此當刀具穿過奇異區域卻不經過奇異點時,加工精度不夠理想。王丹等[10]給出的通用的五軸加工非線性誤差控制算法也可以運用到奇異區域的處理上,但由于單純采用線性插值,使奇異區域內的加工速度大大降低,而且插值過密容易導致機床頻繁地做加減速運動,易引起刀具顫振。
針對以上問題,本文在前人研究的基礎上,以AC 雙轉臺五軸機床為例,給出一種將優化C 軸轉角(簡稱C 角)、修改刀軸方向、遞歸線性插值三者結合的刀具路徑優化算法,從而在提高奇異區域內加工精度的同時,保證速度盡量快、加工更平穩。
1 五軸機床的運動學方程
1.1 AC 雙轉臺五軸機床正向反向運動學變換本文以AC 雙轉臺五軸機床作為研究對象(圖1)。首先根據其機床結構和運動鏈建立機床正向運動學方程。設工件坐標系坐標原點為Ow,工件坐標系下的刀具位置矢量為pw=(xw yw zw)T,刀具方向矢量為uw=(i j k) T;機床坐標系原點為Om,機床線性軸運動矢量為pm=(xm ym zm)T,機床旋轉軸為A 和C,對應的機床轉角分別為α 和γ。
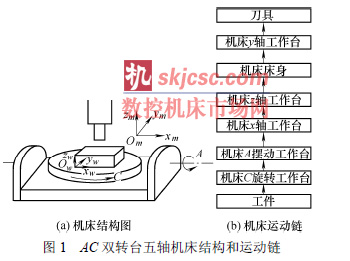
根據圖1 所示的運動鏈,AC 雙轉臺五軸機床的正向運動學方程如下.

由式(3)計算出的原始C 角在(–π, π]之間。由表1 可知,如果相鄰點之間i 或j 的方向發生變化,C角可能會發生劇烈變化。例如第n 點刀軸方向為 (0.100 0, –0.100 0, 0.989 9),第n+1 點的刀軸方向為 (–0.100 0, –0.100 0, 0.989 9),直接依據式(3)計算出來的C角分別為3/ 4π 和−3/ 4π ,相距3/ 2π 。由式 (4)~(7)可知,線性軸的取值與旋轉軸有關,C 角變化劇烈會導致線性軸變化劇烈,從而產生較大的誤差。因此需要對原始的C 角進行修正。由于正弦函數和余弦函數都以2π 為周期,因此利用這一特性在反解三角函數的過程中修改C 角的取值
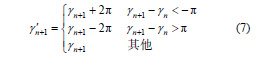
式中 n 1 γ + ′ ——修改后的第n+1 點的C 角取值n 1 γ + ——修改前的第n+1 點的C 角取值n γ ——修改前的第n 點的C 角取值經過這樣處理后,加工路徑上Δγ ( n 1 n γ γ + − )都不超過π ,過大轉角得到初步控制。對于AC 雙轉臺五軸機床來說,C 軸對線性軸的影響大,A 軸較小[11]。因此只需要對C 角進行優化即可。
2 奇異區域內的優化方法
2.1 奇異點和奇異區域
由圖1 可知,當α=0 時,刀軸與轉臺臺面垂直, C 角取任何值刀軸方向都不會改變,造成自由度丟失。根據式(2)~(3)也可以看到,α=0 時,刀具方向矢量為 (0,0,1),此時γ = arctan(0 / 0) ,無解,在Matlab 中規定為0。對于AC 雙轉臺機床,刀軸方向為(0,0,1) 的點就是奇異點。盡管在反運動學變換過程中修正了C 角的取值,但是如果刀具經過奇異點附近即奇異區域時,Δγ 仍然很大,甚至可能達到π 。刀具進入奇異區域后,越接近奇異點,C 角變化越劇烈,由此產生的非線性誤差越顯著,對工件和刀具可能造成的損害也越大。需指出的是,刀具經過奇異區域并不一定會經過奇異點,而經過奇異點就一定是經過了奇異區域。
對于奇異區域的范圍,可以采用基于機床雅可比矩陣條件數的方法來界定:首先根據機床的運動學方程和相鄰點各軸運動變化量建立五軸機床雅可比矩陣,然后求解雅可比矩陣的條件數,如果條件數超過給定值,則可以判定當前加工區間處于奇異區域內[12]。
2.2 奇異點及其附近的C 角處理
造成奇異區域內非線性誤差過大的原因一般有兩個:一是因為奇異點處i 和j 均為0,造成C角值不能確定;二是因為奇異點前后兩點的i 或j可能會發生變號造成的。下面分別就這兩種情況給出處理方法。
2.2.1 第一種情況
對于第一種情況,由于當刀具在奇異點位置時,刀軸與轉臺臺面垂直,C 角無論取何值都不會影響該點的刀軸方向,因此可以指定這一點的C 角值。設指定后的C 角值為γ ′ ,奇異點前后兩點的C角值分別為1 γ 和2 γ 。設定的C 角值要使1 γ ,γ ′ , 2 γ波動最小,需要三者方差最小。奇異點處C 角設定方法如下

這樣,奇異點左右兩個區間的Δγ 都不超過π/2,過大的Δγ 有效降低。表2 給出一處奇異點附近的刀位數據。表3 是對應的機床各軸運動坐標數據。
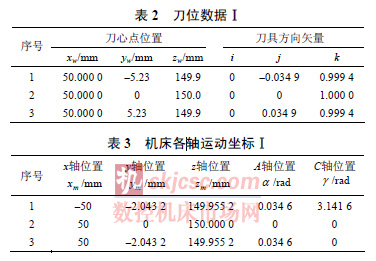
刀具從第1 點走到第3 點,C 角一共變化了π ,但由于第2 點和第1 點之間的Δγ = π ,所以導致這兩點之間的路徑呈現為一個很大的弧。按照上述方法對奇異點處C 角進行設定。之后根據設定的角度修改x,y,z 軸的取值。
表4 給出奇異點處C 角設定后的機床各軸運動坐標。
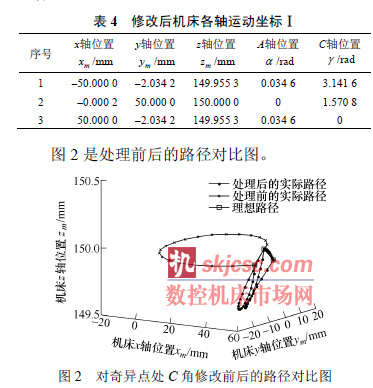
可知,盡管處理后z 軸方向比原先增加了0.3mm 左右的誤差,但是卻使x 軸方向的誤差減小了大約40 mm,y 軸方向的誤差減小了大約20 mm。整體誤差大大降低。
2.2.2 第二種情況
第二種情況是奇異點附近可能會存在軸對稱的點,即位置坐標和方向矢量都關于三維空間某一坐標軸對稱。對AC 機床來說,對稱的兩點z 軸坐標總是相同的,因此只需要研究Oxy 平面上投影的情況。若方向矢量的投影關于y 軸對稱,則i 絕對值相同,符號相反;若方向矢量的投影關于x 軸對稱的兩點,則j 絕對值相同,符號相反。這樣,相鄰兩點的C 角就可能相差超過π/2 。圖3 所示為一種奇異點附近的對稱情況。
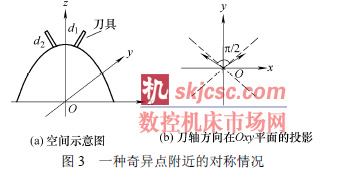
以C 角從第一象限轉到第二象限為例說明。當i ≥ 0且j>0 時,C 角在第一象限,設此時γ =θ 。若i 不變,j 變號,C角轉到第二象限,此時的γ = π −θ 。C角的變化量Δγ = π −θ −θ = π − 2θ 。當| i |≥| j |時,π/4 ≤θ < π/2 , 0 < Δγ ≤ π/2 ; 當| i |<| j | 時, 0 <θ < π/4,π/2 < Δγ ≤ π。因此,當C角從第一象限轉到第二象限時, 若| i |<| j | , 令| i′ |=| j′ |= (| i | + | j |) / 2,就可以保證旋轉不超過π/2 ,其中i′ 和j′ 分別表示修改后刀軸方向矢量在工件坐標系的x 軸和y 軸方向的分量。
同理可得出其他象限的情況,如表5 所示.

需要說明的是,如果兩點不是軸對稱,而是中心對稱,則上述方法無法將Δγ 控制到π/2以內,這時只能通過插值法進行處理。
盡管傾斜刀具可以調整C 角,從而降低非線性誤差,但同時也會帶來過切和欠切誤差。下面通過比較二者的誤差大小來證明傾斜刀軸的有效性。以平底刀為例。設刀具直徑為d,刀具傾斜角為δ ,由此產生的過切和欠切誤差為h。
易知
h = d sinδ (9)
設原來的刀軸方向矢量為a ,修改后的刀軸方向矢量為b ,則sinδ = (| a × b |) /(| a |i| b |) 。由于| a |=| b |=1,所以sinδ =| a × b |。
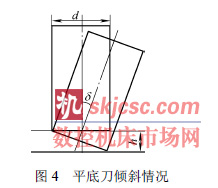
令| k |= 0.995 0 時刀具進入奇異區域,可知0 ≤| i |≤ 0.099 9,0 ≤| j |≤ 0.099 9 。下面分析刀具從第一象限進入第二象限的情況,其他情況同理。當前一點刀軸矢量為(0, 0.099 9, 0.995 0),后一點刀軸矢量為(0, –0.099 9, 0.995 0)時,Δγ = π,變化量最大。根據上面方法對前后兩點分別進行修改。前一點為(0.05, 0.05, 0.997 5),后一點為(0.05, –0.05, 0.997 5)。sinα = 0.070 5。若平底刀直徑取6 mm,則過切和欠切誤差h=0.423 mm。也就是說,對于直徑6 mm 的平底刀,修改刀軸方向引入的最大過切和欠切誤差為0.423 mm,而過大的C 角由π 降到π/2 ,由此降低的非線性誤差遠大于新引入的過切和欠切誤差。因此在奇異點附近傾斜刀軸是有效的。表6 給出一處奇異點附近的刀位數據。表7 是對應的機床各軸運動坐標。
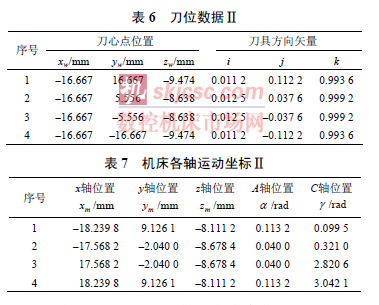
由表4 可見,由于j 符號發生變化,且| i |<| j |,第2 點和第3 點間的C 角變化超過π/2 。同時看到第1 點與第2 點以及而第3 點與第4 點間的變化很小,因此可以考慮修改第2 點和第3 點處的刀軸方向,適當增加其他兩個區間的C 角變化量,來降低奇異點附近的過大C 軸轉動8 為修改后的刀位數據。表9 為對應的機床各軸運動坐標。
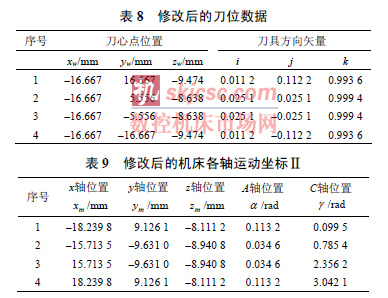
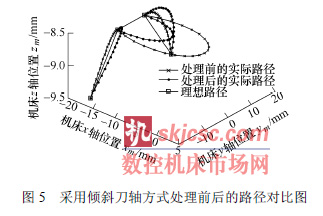
圖5 是傾斜刀軸前后的路徑對比圖。4 個點的C 角方差由修改前的2.484 5 降到1.854 4,波動變小。最大非線性誤差由16.680 8 mm 降到8.810 4mm,平均誤差也由6.075 5 mm 降到4.903 3 mm。使用直徑6 mm 的平底刀,傾斜刀軸所引入的過切和欠切誤差僅為0.106 8 mm。由此可見,整體誤差大大降低。
2.3 遞歸插點
經過以上處理后,大部分Δγ 都降到π/2以下(除非存在中心對稱的刀位點)。如果還需要進一步提高加工精度,則通過插點對加工路徑進行線性化。
設相鄰兩個刀位點為( w, w ) p′ u′ 和( w, w ) p′′ u′′ 。設實際加工路徑的中點與編程直線的中點之間的距離為r 。最大允許誤差為ω 。若r >ω ,在相鄰刀位點中點處插入新的刀位點( pw,uw ),然后檢查( w, w ) p′ u′ 與 ( pw,uw )之間、( pw,uw )與( w, w ) p′′ u′′ 之間的非線性誤差是否超過ω 。如此遞歸進行,直到r ≤ω 。
插入新刀位點時將刀具的位姿同旋轉軸的轉角結合起來考慮,具體方法如下:設(α0 ,γ 0 ) 和 (α1,γ 1)分別為刀位點( w, w ) p′ u′ 與( w, w ) p′′ u′′ 所對應的旋轉軸轉角坐標。首先,計算(α0 ,γ 0 )和(α1,γ 1)的中值對應的方向矢量w u ,然后求w ′p 與wp′′的中值pw,最后將pw與uw組成新刀位點( pw,uw )。若直接令w ( w w ) / 2 p = p′ + p′′ ,再用式(2)和式(3)求解中點處的α 、γ ,則不能有效降低誤差,原因是奇異區域內分量i 和j 接近0,造成C 角值偏差很大。
2.4 整體優化流程
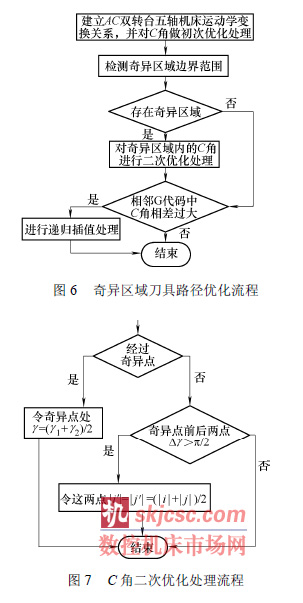
綜上所述,奇異區域的優化處理流程如圖6 和圖7 所示。
3 加工試驗
下面通過仿真試驗和實際加工對上文給出的算法進行驗證。選擇直徑6 mm 的球頭刀進行加工。加工曲面S(u,v)的參數方程如式(10)所示
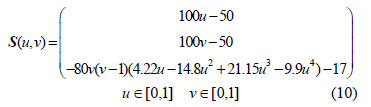
式中,u, v 為曲面方程的參數。表10、11 給出初始刀位點和初始機床各軸運動坐標。可以看到奇異點附近的兩種情況所導致的C 軸過大偏轉。

圖8 所示是所給加工曲面的Matlab 仿真效果圖。經過對C 角初步優化后,過大的環形軌跡得到初步控制,再通過二次優化和插值處理,得到的路徑與理想路徑基本接近。

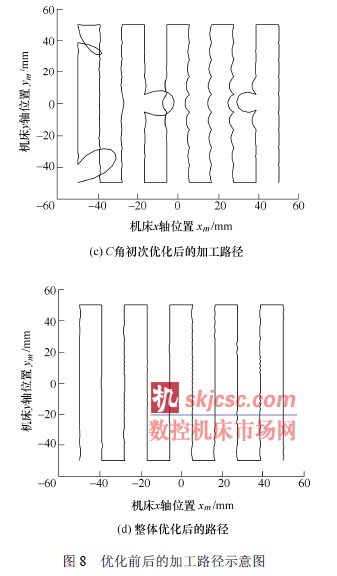
實際加工的路徑對比如圖9 所示。圖9a 實線圈出的是奇異區域內的過大環狀軌跡,其中靠下面的兩個是第一種情況,靠上面的兩個是第二種情況。可以看到,處理后加工路徑更加平滑,加工精度大大提高,實際的加工情況與理論分析結果一致。需要說明的是,由于過大環形軌跡會對刀具造成損害,因此未對圖8b 所示的情況進行實際加工。采用直接插點法,需插入737 個點才能將最大非線性誤差降到0.099 8 mm。而采用綜合方法處理時,新插入點304 個,最大非線性誤差0.098 4 mm,速度是直接插點法的二倍。

4 結論
(1) 本文在對奇異區域內五軸加工過程的處理上,根據相鄰點C 角變化量大小,依次進行C 角的初次優化、C 角的二次優化、加工路徑線性化處理。盡管這個過程會引入新的過切和欠切誤差,并且為了降低某一個區間的過大誤差而增加了其他區間的誤差,但是整體的誤差得到了有效控制,同時增加的誤差也在允許范圍內。
(2) 這種處理方式既保證了奇異區域內的加工精度,有效地保護了工件和機床部件,又盡可能地減少了插點的數量,使奇異區域內的加工速度盡量提高。
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com










