0 引言
滾珠絲杠副是數控機床及加工中心的關鍵部件, 起到精密傳動和定位的作用。數控機床向高速高精方向的發展對滾珠絲杠的精度提出了更高的要求。研究滾珠絲杠的溫升及熱變形規律對提高機床的加工精度具有重要意義。在這方面, 前人已有一些有意義的工作。Huang[ 1] 把滾珠絲杠前后軸承、絲杠螺母等熱源處的溫度作為預測模型的變量, 用多元線性回歸的方法較好地預測了滾珠絲杠在不同轉速下的熱變形。Kim 等[ 2] 與Wu 等[ 3] 通過有限元方法研究了施加軸向預負載的滾珠絲杠在不同轉速和運行時間下的溫度分布, 并將其與實驗結果進行了比較。宋現春等[ 4]分析了精密絲杠磨削過程中引起工件熱變形的主要因素, 提出了通過控制磨削溫度來減小和控制工件熱變形的方法和途徑。以上方法主要考慮的是機床由熱變形產生的靜態誤差或準靜態誤差通過經驗建模得到絲杠系統的測點溫度變化和關鍵點熱變形之間的關系模型, 從而獲得補償策略并通過控制系統對熱誤差進行補償。然而經驗建模方法對工作條件變化范圍大、時變性強的工況來說, 其精度和魯棒性很差。隨著工況和環境的變化, 機床的熱源也是動態變化的, 研究多變化熱源產生的溫度場和熱變形的動態特性, 可以更準確對機床熱誤差進行實時補償, 進一步提高機床加工精度。
本文以傳熱學理論為基礎, 探討了滾珠絲杠受多變化熱源影響而產生的溫度場及熱變形的動態特性, 并通過有限元軟件進行仿真, 研究了滾珠絲杠在特定工況下產生的溫度場、熱變形場及其變化規律。
1 滾珠絲杠熱傳導的理論問題
1. 1 熱傳導方程
滾珠絲杠系統的熱源主要有端部驅動電機功率損耗產生的發熱、絲杠兩端軸承摩擦發熱、絲杠與絲杠螺母摩擦發熱。首先, 考慮端部電機和軸承發熱對絲杠熱變形的影響。由于影響機床加工精度的主要是軸線方向的熱變形, 因此不考慮絲杠徑向方向的熱變形。
絲杠長為L , 它與周圍空氣的熱對流系數為as , 周圍空氣溫度為Hf , Q( t ) 為從絲杠左端流入的周期變化熱源。圖1 中絲杠的熱傳導方程為[ 5O7]

1. 2 溫度響應
通過監測熱源處的溫度值來評價熱源的發熱強度。在絲杠左端A 處輸入周期變化的熱流, 監測得A 處的溫度變化函數為
H( x , t) | x= 0 = H( 0, t) = H0 + H1 sin( Xt - U) ( 3)
則式( 3) 為式( 2) 的邊界條件。可求得式( 2) 的解
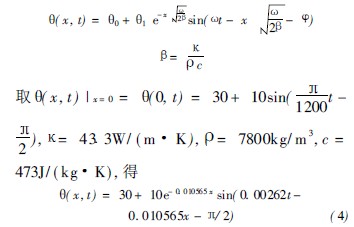
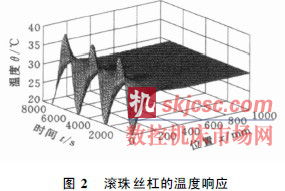
式( 2) 的求解使用了式( 3) , 而沒有用任何其他初始條件, 這類方程適合于求解機床達到準穩態時周期變化熱源產生的溫度響應。根據式( 4)可分別繪制滾珠絲杠的溫度響應圖( 圖2) 和不同位置的溫度變化曲線( 圖3) 。
從圖3 可知, 溫度的幅值隨著x 的增大而減小。不同位置x 處的溫度曲線具有相同的周期, 但相位角U不同, 隨著x 的增大, 相位角U也增大, 表現出了明顯的滯后性。
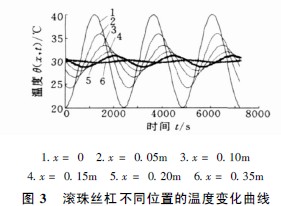
由式( 4) 及圖2、圖3 可知, 溫度H( x , t) 隨距離x 按周期分布, 溫度波的振幅隨x 而減小, 振幅為

1. 3 任意熱源信號的溫度響應
根據工況不同, 機床熱源的變化情況主要可分為周期性熱源和非周期性熱源。加工多零件、多工序時可能出現周期變化或準周期變化的熱源。按熱源波形劃分又有斜波、方波、余弦波等不同的周期熱源。熱源函數H( x 0 , t) 在時間上是連續的,滿足Dir ichlet 條件, 在時間域內可以展開成關于時間變量t 的傅里葉級數, 即
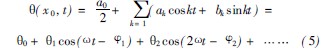
單工序時機床可能出現非周期性的線性熱源或其他非線性熱源, 先對熱源函數進行奇拓展( 或偶拓展) , 再由傅里葉公式展開成余弦級數。故考慮機床余弦周期熱源的響應問題具有較普遍的意義。將式( 5) 代入式( 2) , 可求解滾柱絲杠對于任意熱源信號所產生的溫度響應:
![]()
1. 4 多熱源融合
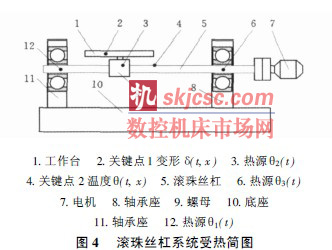
如圖4 所示, 滾珠絲杠系統中, 主要有電機、兩個軸承和絲杠螺母產生的4 個熱源, 這里把電機和與電機相鄰軸承的生熱之和當作一個熱源來考慮, 為H3 ( x , t) , 另一軸承產生的熱源為H1 ( x , t) , 絲杠螺母處的熱源為H2 ( x , t) 。由于導熱方程是線性方程, 它滿足疊加原理[ 8], 即幾個熱源同時作用下的溫度響應等于各個熱源作用下溫度響應的疊加。由式( 6) , 得

雖然動態、時變熱源產生的溫度場是非常復雜的, 但常用器件如電動機、軸承等的發熱規律是可計算和預測的[ 9, 10] , 通過監測熱源處的溫度變化規律并結合式( 5) 、式( 7) , 可初步確定滾珠絲杠的溫度場分布。
2 滾珠絲杠系統多熱源溫度場及熱變形仿真
2. 1 構建模型及加載
在幾何建模及加載時做了一些簡化, 忽略了絲杠上的螺紋槽, 把滾珠絲杠簡化成一個狹長的圓柱體。模型如圖5 所示, 采用SOLID5 熱- 應力耦合單元劃分中心對稱的網格。

滾珠絲杠圓柱面與周圍空氣的對流換熱系數為121 5, 空氣溫度為20 e , 鑄鐵導熱系數為70W/ ( m # K) 。在模型的節點上添加的均一溫度負載為20 e 。兩端面添加的周期性溫度載荷( 通過ANSYS81 0 里的函數編輯器可以定義多種函數表達的載荷) 為
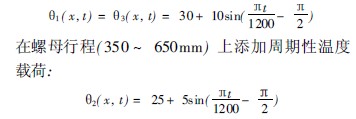
2. 2 多熱源滾珠絲杠溫度場仿真
把建好的模型用求解器進行求解, 對模型進行瞬態溫度場的分析。時間終點為7200s, 時間步長為72s。由于H1 ( x , t) = H3 ( x , t) , 滾珠絲杠軸向溫度分布具有對稱性, 故只考慮x I ( 0, 01 40)m范圍內的溫度分布。求解可得如圖6 所示的分析結果。
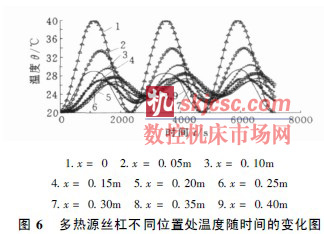
由圖6 可知, 不同位置處的溫度以2400s 為周期; x 在0 ~ 01 30m的變化范圍內, 幅值從40 e 衰減到大約261 5 e , 在01 30 ~ 0140m 的變化范圍內,幅值從大約2615 e 又增加到大約30 e 。由于熱源H1 ( x , t) 和H2 (x , t) 的共同作用, 溫度波在x I ( 0, 01 25)m 內向右移動, 在x I ( 01 25, 0140)m內向左移動。
2. 3 多熱源滾珠絲杠熱變形仿真
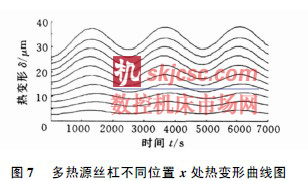
對圖5 中的模型進行溫度- 應力耦合分析,時間終點為7200s, 時間步長為72s。圖7 所示的10 條曲線從上至下依次為x =11 0m, x = 01 9m, x = 01 8m, x = 01 7m, x =01 6m, x = 01 5m, x = 01 4m, x = 01 3m, x =01 2m, x = 01 1m 時的滾珠絲杠熱變形隨時間變化的曲線( 圖7 中熱變形包含絲杠從0 e 升高到20 e 的值) 。比較這10 條曲線, 發現不同的x 處存在熱變形波移動的現象, 由于熱源H1 ( x , t) 、H2 ( x , t) 和H3 ( x , t ) 的共同作用, 溫度波在x I ( 01 1, 01 3) m 范圍內向右移動, 在x I ( 01 3, 01 7)m 范圍內向左移動, 在x I ( 01 27, 11 0) m 范圍內又開始向右移動。
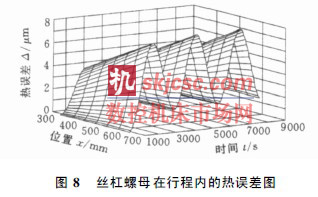
滾珠絲杠產生的熱誤差通過絲杠螺母傳遞給工作臺。通過對有限元分析結果進行一定的處理可得圖8 所示的絲杠螺母在行程x I ( 350650) mm 內的熱誤差圖。由圖8 可知, 熱變形誤差沿時間軸具有明顯的周期性, 且周期為2400s; 曲線的幅值隨x 增大線性增大, 在行程內, 幅值由3Lm 增加到7Lm; 圖8 清晰顯示出了絲杠螺母軸向熱誤差隨時間t、軸向距離x 的變化關系及動態特性, 為進一步制定誤差補償策略奠定了基礎。
3 結論
本文用傳熱學的理論研究了滾珠絲杠受周期變化的端熱源影響而產生的溫度響應及其變化特性, 采用疊加法求解多變化熱源作用下滾珠絲杠的溫度場; 通過有限元仿真, 進一步驗證了理論結果的正確性, 得出了滾珠絲杠在行程內熱誤差動態變化的曲面圖。在研究工作中忽略了滾珠絲杠與周圍空氣的熱交換、簡化了滾珠絲杠結構上的許多細節, 這與絲杠系統的實際工況有一定的差異, 但這并不妨礙滾珠絲杠溫度場和熱變形變化規律性研究的正確性。
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com










