一区免费视频_亚洲精品成人av在线_久久99国产精品久久99果冻传媒_毛片网站多少

      0 引言

      金屬切削加工過程是一個非常復雜的動態性、非線性的工藝過程，常伴隨著切削力、切削熱和刀具磨損等物理現象。其中，切削熱是一個重要的物理參數標志，它直接影響著刀具的磨損、刀具的使用壽命、工件的加工精度以及加工表面的完整性[1,2]。因此，切削溫度場的理論研究對分析金屬加工原理、預測工件的加工精度以及刀具磨損機理等方面具有重要的意義。

      目前，常用的切削溫度場研究方法主要有：試驗法（如：人工熱電偶測溫法、紅外熱像儀法等）、解析法（如：積分變化法、拉普拉斯變化法）和有限元數值法（如：有限差分法、有限元法[3]）。試驗法可以得到可靠的數據，但是試驗法無法直接得到溫度場的分布情況，只能測得某點處的平均溫度（如：人工熱電偶法）；解析法常常基于各種假設，與實際情況不符；有限元法在解決由材料性質、變形狀態和多耦合場引起的非線性問題時，往往表現出其獨特的優點，更加接近于實際，同時有限元法可以快速地得到精確的仿真結果[4,5]。綜上所述，本文采用有限元數值分析模擬切削加工過程中的溫度場分布情況，并與試驗結果進行比較。

      1 切削熱的產生與傳出

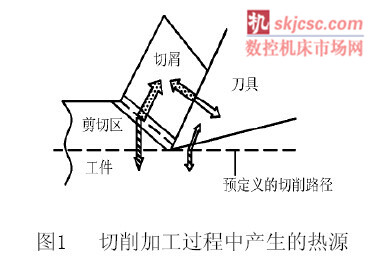
      金屬切削加工時，切削熱主要來源于三方面：由于切屑最底層金屬材料的摩擦和擠壓變形所產生的切削熱、刀具克服切削層金屬的剪切變形做功所產生的切削熱以及刀具與已加工表面的摩擦擠壓變形所產生的切削熱。因此根據上述分析將切削加工時產生的溫度場劃分為三類，即：剪切區溫度場、刀具與切屑接觸區溫度場以及刀具和工件接觸區溫度場, 如圖1所示。

      切削加工過程中，切削熱大約有80%的熱量由刀具克服工件彈塑性變形產生，約18%的切削熱有切屑底層材料與刀具間摩擦產生，約2%的熱量刀具與已加工表面間的摩擦產生[6]。大部分切削熱由切屑帶走（約95%的熱量），只有少部分熱量殘留于工件內。

      2 正交切削模型的建立

      金屬切削加工時，刀具的主切削刃和副切削刃都參與切削成形，如果車削仿真過程中，同時考慮主、副切削刃參與切削時，會造成金屬層在主、副切削刃交匯處產生干涉，從而影響仿真效果。因此本文采用正交切削模型進行仿真。

      假設整個仿真過程中，工件材料與刀具材料導熱各向同性，且無內熱源，金屬切削瞬態溫度場應該滿足二維導熱微分方程：

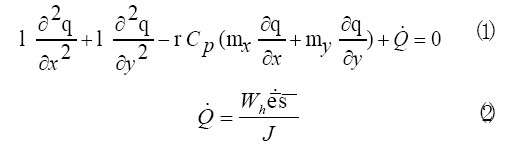
      其中：公式（1）與公式（2）中1為熱傳導率；C為比熱； r 為材料密度；為單位體積的熱產生率；為塑性變形轉化為熱的比率，本文設定為0.9，為等效應力；為等效應變速率；J為熱功當量系數。

      2.1 改進的Lagrange網格劃分方法

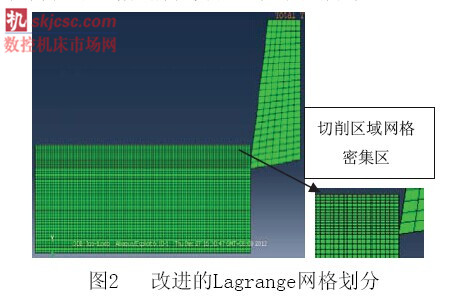
      金屬切削過程是一個典型的局部變形過程，工件的幾何形狀與尺寸隨仿真時間不斷發生變化，并且隨著變形的加劇，為了避免仿真時網格發生嚴重的扭曲變形，采用改進的Lagrange網格劃分方法，該方法將Lagrange法和Euler法有效地結合在一起，這樣劃分的網格不會像純拉格朗日方法出現網格始終跟隨材料流動，也不會出現像純歐拉方法網格始終固定不動[7~9]。同時為了節約仿真時間和計算機存儲空間，網格的劃分并不是均勻的，而是靠近切削部分的網格劃分較細，遠離切削部分的網格劃分較疏，如圖2所示。

      2.2 摩擦模型的建立

      由Zorev[10]提出的摩擦模型表明：切屑與刀具前刀面接觸區域內存在兩種不同的接觸狀態，即滑動區和黏結區，在黏結區內的各點的切應力基本相同；滑動區內的摩擦應力沿刀具前角而減小，滿足庫倫摩擦定律。即：

      其中：公式（3）中 為刀屑接觸面的摩擦應力；m為摩擦系數； 為刀屑接觸面的正應力；為切削材料剪切流動應力。

      本文在ABAQUS/Explicit仿真器下，刀—屑接觸區采用面對面接觸（Surface to Surface contact）接觸類型采用運動學接觸方式（Kinematic contactmethod），采用有限滑移方式（Finite sliding），權重因子系數設為0.5。滑動區和黏結區的摩擦系數分別設定為0.4和1。在ABAQUS/Explicit仿真器中，可以根據實際的接觸應力來判斷刀具與切屑之間處于何種接觸，從而選擇其相對應的摩擦模型，圖3是AISI1045鋼摩擦模型的接觸關系。

      2.3 邊界條件設定

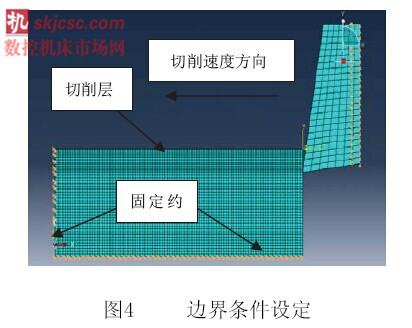
      工件的尺寸設定為15mm×7.5mm。切削速度方向沿著X軸的負方向，固定工件底邊和左邊的X、Y、Z方向上的平移和轉動自由度。設置工件和刀具的初始溫度為室溫20℃，分別定義兩個接觸邊界條件，分別為刀具/工件接觸條件和工件/工件自接觸條件，切屑層網格在刀具前刀面的剪切作用下變形成剪切層，剪切層與切削速度方向之間的夾角為剪切角，如圖4所示。

      2.4 本構模型的選擇

      金屬材料切削時通常在高溫、高壓、大應力及大應變率的環境條件下，為了使仿真結果更加貼近實際，采用Johnson-Cook模型，該模型是一種用于描述金屬在大變形、高應變率效應和高溫條件下具有良好特性的本構模型，該方程構造簡單，應用范圍廣泛，一般適用于應變率在一個較大范圍內內應力、應變變化的情況[11]，其表達式如下： 

      3   AISII045鋼切削溫度場仿真結果與試驗分析

      根據上述分析，建立了正交切削有限元模型，得到了AISII045鋼切削溫度場的分布狀況。

      3.1 溫度場分析

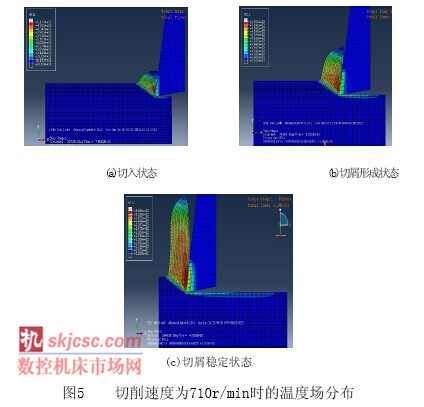
      圖5是刀具切削AISII045鋼仿真得到的溫度場云圖。從該云圖可以看出：切削過程中產生的切削熱大部分被切屑帶走并且從切削開始到穩定切削時，溫度場的分布狀況可以分為四個階段：

      第一階段：初始階段，如圖5（a）所示，切削熱主要產生在第一變形區，并且靠近前刀面處切屑上出現了溫度密集區，這是由于刀具克服第一變形區內的金屬材料大塑性變形而作功產生較高的切削熱。

      第二階段：切屑的形成階段，如圖5（b）所示，切削熱集中區域轉移到第二變形區，且溫度最高點并不在刀尖處而是在離刀尖2~3mm。這是由于刀具克服第一變形區內的金屬材料大塑性變形而作功產生較高的切削熱。刀具前刀面和切屑之間存在著強烈的摩擦，由于摩擦生熱使得刀—屑接觸區產生較高的切削熱。

      第三階段：隨著切削過程的進行，切屑進一步形成階段，如圖5（b）所示。切削熱的集中區域向第三變形區擴展，這是由于已加工表面與后刀面摩擦而產生切削熱。

      第四階段：切屑成形已經進入穩定狀態，如圖5（c）所示，第二變形區和第三變形區的切削熱逐漸沿前刀面向上和沿后刀面向右擴散。這是因為切削速度太快，使得切屑與前刀面或已加工表面和后刀面形成的切削熱來不及擴散，從而殘留在切屑和已加工表面上。

      從圖6的溫度場等值線可知存在很高的溫度梯度曲線。由于第一變形區金屬材料的大塑性變形而產生了較高的熱能，故在刀尖處出現了較高的切削溫度；刀具前刀面與切屑間的強烈摩擦熱及切屑變形熱作用，則在刀尖偏上位置產生了第二高溫區，而除此之外的部分的溫度相對較低。

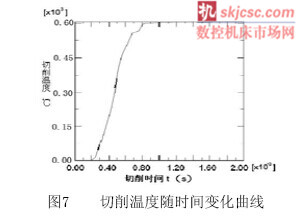
      從圖7切削溫度曲線可知：前刀面最高溫度為533.2℃，刀尖處溫度為342℃。在切削達到2×10-3s時，溫度曲線趨于穩定。此時大部分熱能由切屑帶走，所以溫度不在上升，從而趨于平穩。 

      3.2 試驗結果對比分析

      為了驗證仿真結果，對切削溫度進行了試驗驗證，本試驗在CAK 5085dj車床上進行，工件材料為AISI-1045鋼，工件直徑d=40mm，采用人工熱電偶法對切削溫度進行測量，測量結果如圖8、圖9、圖10所示。

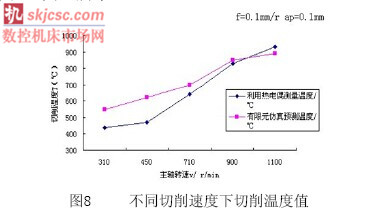
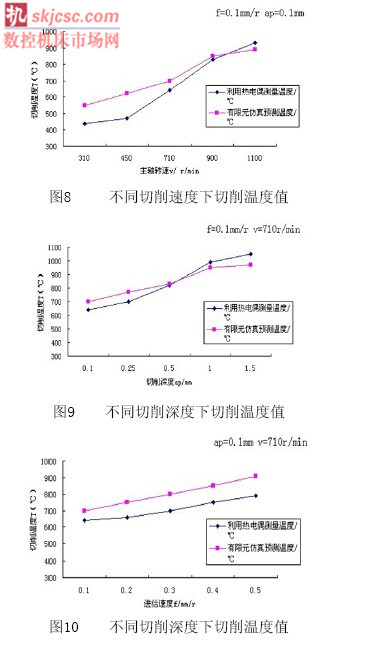
      通過對比發現，所有的仿真結果跟試驗結果都非常吻合，這說明所建立的有限元模型不僅可以得到較為準確的溫度場數值，而且在不同參數下其仿真結果同樣準確，從上圖中不難看出：對切削溫度場影響較大的因素為切削速度、切削深度和進給量。隨著切削速度、切削深度、進給量的不斷增加，切削溫度也是不斷增加的。

      4 結論

      1）通過利用有限元法仿真得到的切削溫度值和實測值對比表明：在試驗數據范圍內，該方法具有很高的預測精度。且它相對應于其他方法（如：試驗法、解析法）可以得到金屬車削過程中無法直接測量或根本測量不到的溫度場分布情況。

      2）從仿真結果和實測值可以看出：實際切削加工中，對溫度場影響加大的因素為切削速度、進給量和切削深度，隨著切削三要素的增加，切削溫度呈現增大的趨勢。

      3）本文建立的二維溫度場模型與實際情況是相符的，但是如果需要進一步考慮刀具斜角對切削溫度場影響情況時，可以選擇建立三維模型進行研究，這部分工作也具有重要的物理意義和應用價值。