對于一般的機械系統,應從系統工程學及工程價值學的觀點去解決該系統機電及其他物理參數的協調和匹配的分析與綜合問題。研究這種分析與綜合的方法和理論就導致了機電一體化學科的形成和發展。機器人系統就是一個極其典型的機電一體化系統,機器人運動學及動力學則為這種系統的機電一體化的分析與綜合提供必要的預備理論知識[1]。作者將機器人運動學的研究方法運用到加工中心中去。
機器人的運動學方程是表示機器人操作機或機械手每個桿件在空間相對于絕對坐標系或相對于機器人機座坐標系的位置及方向的方程[2]。對于加工中心來說,就是把具有相對運動的各個部件看成桿件,用方程來表示銑頭刀尖點相對于機床坐標系的位置和方向。
1 加工中心運動學方程的建立
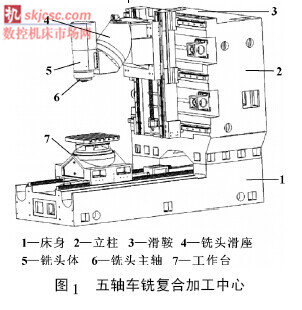
根據五軸加工中心的結構特點( 如圖1 所示) ,建立D-H 坐標系( 如圖2 所示) ,求解加工中心的運動學參數。圖中,{ M} 為機床坐標系,{ W} 為旋轉工作臺坐標系, { T} 為刀具坐標系,xiyi zi為中間坐標系,i = 1,2,3,4。
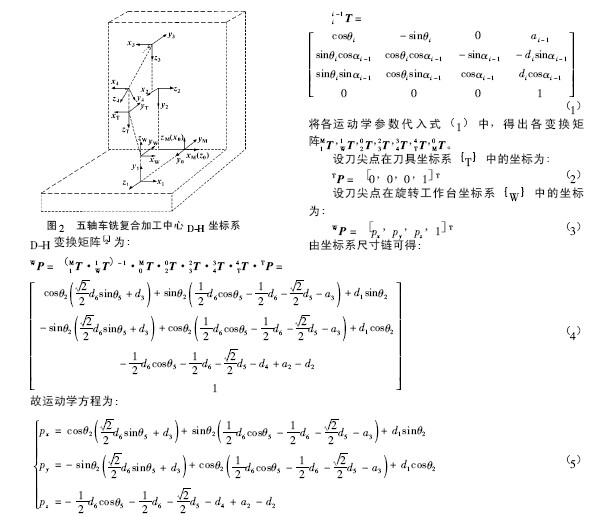

(1) 運動學方程的正解
當加工中心操作機構的結構參數已確定,并給出各運動關節的運動參數,就可確定加工中心末端執行器在機座坐標系中所處的位置和姿態,這就是求解加工中心運動學的正問題,也稱直接位置求解。運動學正問題的求解方法是利用其運動學方程進行坐標系的連續變換,即變換矩陣的連乘,計算出矩陣中每個元素的值,它們就表示了在指定的參考坐標系中,加工中心末端執行器的位置和姿態。矩陣是唯一的,因此在驅動裝置作用下操作機動作時,就給定了一組結構參數和運動參數,加工中心運動學方程的正解也是唯一的。
(2) 運動學方程的逆解[3]當加工中心末端執行器的位置和姿態給定時,如何求出各關節變量,這就是求解加工中心運動學的逆問題,也稱間接位置求解。根據式( 6) 兩端矩陣元素應相等的原理,可得一組多變量的三角函數方程。求解這些運動參數,需解一組非線性超越函數方程。求解方法有3 種: 代數法、幾何法和數值解法。前兩類方法是基于給出封閉解,它們適用于存在封閉逆解的加工中心。關于加工中心是否存在封閉逆解,對一般具有3 ~ 6 個關節的加工中心,有以下充分條件:①有3 個相鄰關節軸交于一點; ②有3 個相鄰關節軸相互平行。只要滿足上述一個條件,就存在封閉逆解。如CX 五軸車銑復合加工中心就滿足第二個條件。數值法由于只給出數值,無需滿足上述條件,是一種通用的逆問題求解方法,但計算工作量大,目前尚難滿足實時控制的要求。
下面介紹代數法中的遞推逆變換法。將一組逆矩陣連續左乘式( 6) 兩端,可得若干矩陣方程,每個矩陣有12 個方程式; 在這些關系式中可選擇只包含一個或不多于兩個待求運動參數的關系式,然后遞推求解,一般遞推過程不一定全部作
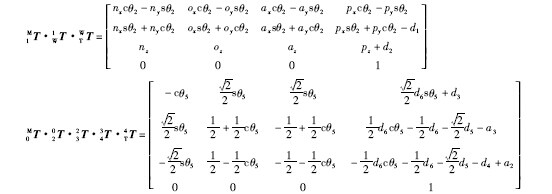


它是衡量加工中心工作能力的一個重要運動學指標。加工中心的工作空間定義為: 加工中心正常運行時,末端執行器坐標系的原點能在空間活動的最大范圍。這一空間又稱可達工作空間[4]。目前求解工作空間的方法有很多,這里分別運用蒙特卡洛法和極限邊界數值搜索法來求解,具體方法如下:
(1) 蒙特卡洛法。各關節變量在各自范圍內隨機取值,代入運動學方程求出運動學正解,即得到末端三維坐標。
(2) 極限邊界數值搜索法,也稱窮舉法。首先求解運動學逆解,然后在一定的范圍內取樣,通過運動學逆解來確定各運動學參數,再根據約束條件來判斷是否在工作空間之內,由此搜索符合條件的點即構成工作空間。
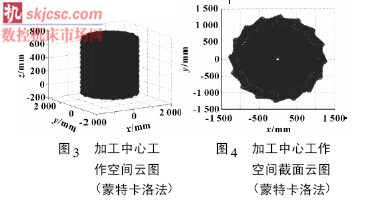
首先運用蒙特卡洛法,具體方法為讓各運動參數在各自范圍內按照一定步長取值,然后求得相應的運動方程的正解,也就得到了加工中心末端點的三維坐標值,將這些點用圖形表示出來即可得到加工中心的工作空間[5],如圖3、圖4 所示。
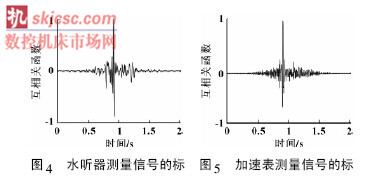
為了評估SCOT 加權廣義互相關算法的精確度,d1被計算出來。針對水聽器的測量信號,分辨率為Δτ = 0. 017 s,計算得d1 = 73. 3 cm,相對誤差為0. 27%。針對加速表的測量信號,分辨率Δτ = 0. 006s,計算得d1 = 73. 6 cm,相對誤差為0. 14%。
利用式( 8) 計算SCOT 加權廣義互相關算法的方差。水聽器測量信號的標準偏差為- 0. 092,其標準偏差很小。加速表測量信號的標準偏差是- 0. 092,其標準偏差也很小。由于帶通濾波器的存在,相對于SCOT 加權廣義互相關算法的分辨率,其標準偏差是無關緊要的,并且在今后的船舶管系泄漏定位的實際操作中可以將其忽略。
4 結束語
在船舶復雜的背景噪聲中,船舶管系泄漏定位是船舶裝備監控系統中的重點,也是實現的難點。通過廣義加權互相關法,選擇SCOT 加權函數,可以有效地抑制背景噪聲對泄漏信號的影響,突出互相關函數峰值,提高定位的準確性。通過實驗驗證,SCOT 加權廣義互相關算法可很好地用于船舶管系泄漏定位,表現出了相對較好的魯棒性。
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com










