超精密車床主軸回轉誤差測試系統的研究
2016-12-14 來源:哈爾濱工業大學 作者:王世良
第 4 章
傾角運動誤差分離及實驗研究
本章將主要分析主軸傾角運動誤差,在徑向運動誤差的基礎上推導傾角運動誤差求解算法;進行超精密車床主軸傾角運動誤差實際測量實驗,并對不同轉速下主軸傾角誤差運動進行研究。
4.1 傾角運動誤差分析
4.1.1 軸線平均線的確定
為理解軸線平均線,我們先看一下國際機械生產研究學會(CIRP)對回轉軸線的定義。1976 年 CIRP 發表了“關于回轉軸性能的描述和測定”的統一文件,定義了回轉軸線,即“回轉軸線是一條某指定物體繞其自身旋轉的線段,此線段與該指定物體一起運動,并相對于軸線平均線呈現出軸向、徑向和角向的運動。”文件對回轉軸的回轉軸線給出了以上明確定義,但是并沒有對回轉中心給出明確定義[48]。
回轉軸線是回轉軸在任意一個瞬時具備的屬性線,軸線平均線是一段時間內對回轉軸線位置進行平均化得到的。在超精密車床主軸回轉誤差測量中,信號的同步運動誤差,即是將主軸的回轉誤差運動作為周期性誤差運動處理。在同步誤差運動中,軸線平均線即為主軸周期性回轉一周時,回轉軸線的平均位置。

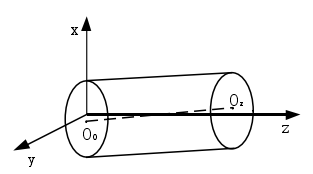
圖 4-1 回轉體軸線平均線模型

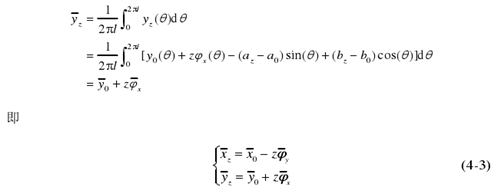
在上述方程處理過程中,我們假設回轉軸的回轉運動具有周期性。實際超精密車床主軸回轉誤差測量中,我們提取主軸的同步運動誤差,實際上就是將主軸的回轉誤差運動作為周期性運動處理的。方程(4-3)為一空間直線方程,從方程中看出,任意截面中的任意點在回轉軸回轉一個周期內平均位置不變,這個平均位置點即為平均回轉中心。雖然在推導過程中,應用的是最小二乘圓心,但是沒有用到最小二乘圓心的任何性質,對截面內任意一點,公式依然成立。上式中的空間方程即為軸線平均線,由平均回轉中心組成。
從以上分析和概念可知:已知截面內任意一點的運動軌跡,可求出此截面的平均回轉中心;軸線平均線是一條空間直線,即各個截面求出的平均回轉中心在一條空間直線上。所以說,已知任何兩截面中任一點的運動,都可以唯一的求出回轉軸的軸線平均線。而軸線平均線是求回轉軸傾角運動誤差的絕對參考線,每個時刻回轉軸的瞬時回轉軸線與平均回轉軸線有一個相對位置。
4.1.2 雙截面測量坐標系的相對位置
回轉軸每個瞬時的回轉軸線與軸線平均線有一個傾角關系。回轉軸線是在雙截面中的兩個測量坐標系中確定的,而平均回轉軸線在空間中是固定的,處于固連在大地上的絕對坐標系中。所以在計算傾角誤差之前首先要明確的是測量坐標系與絕對坐標系的位置關系。
測量坐標系不能簡單地理解成由傳感器的布置決定,也不要簡單地把三個傳感器軸線的交點當成測量坐標系的原點。以下將對這兩個誤區進行分析。
傳感器布置如圖 4-2 所示,兩傳感器相互垂直對截面進行測量。建絕對立坐標系 2,其原點是該截面最小二乘圓心回轉一周的平均位置。坐標系 1為測量坐標系。水平和垂直方向上的傳感器測量值記為S1(θ) 、S2(θ)。
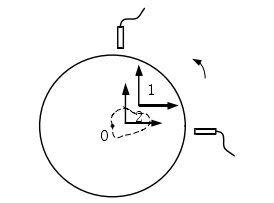
圖 4-2 測量坐標系與絕對坐標系的位置關系


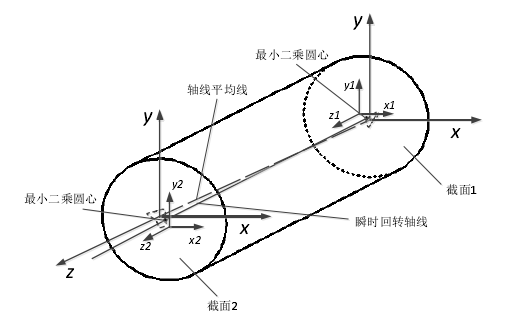
圖 4-3 雙截面測量坐標系與絕對坐標系的位置關系
4.1.3 傾角運動誤差計算
定義回轉軸的軸線平均線的意義在于給出決定傾角誤差運動的參考基準,以軸線平均線建立絕對坐標系,在此坐標系中計算回轉軸回轉周期內的傾角運動誤差。傾角運動誤差即是回轉軸每個瞬時的回轉軸線在絕對坐標系中對x 軸和 y 的轉角關系。
計算回轉軸的傾角運動誤差要對回轉軸的兩個截面的回轉運動誤差進行測量,對兩個截面的數據進行綜合處理得出傾角運動誤差。當回轉軸以一定轉速穩定轉動后,其軸線平均線在空間中是一條固定的直線,基于此線建立絕對坐標系。每個截面由傳感器的安裝位置各自決定此截面的測量坐標系,兩個測量坐標系在絕對坐標系中處于不同的位置。
兩個截面數據要進行綜合處理的一個非常關鍵的因素是確定兩個截面的測量數據要轉化到一個坐標系中進行處理,否則結果就是失真的。測量數據是依賴于測量坐標系的,根據上節的結論,去掉直流分量的傳感器測量值將依賴于絕對坐標系(測量坐標系與絕對坐標系重合),測量坐標系在絕對坐標系中的位置,所以可以將測量坐標系的數據轉化到絕對坐標系中進行求解。
第一個測量截面為定義為基準面,在此截面上測量的徑向運動誤差將作為基準,通過第二個截面的徑向運動誤差來求得主軸的傾角運動誤差。




主軸的兩個截面上的徑向運動誤差相差很小,對于一般主軸差值是微米級,對超精密車床來說此差值的數量級都是在亞微米級。而兩個測量截面的間距 l 是毫米級或是更大,所以公式(4-4)和公(4-5)可做如下簡化為
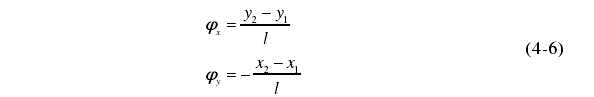
4.2 傾角運動誤差測量實驗及分析
4.2.1 傾角運動誤差測量實驗方案
傾角誤差是指主軸軸線繞 x,y 軸的轉動傾角,測量時要對被測試件垂直于軸線的兩個截面進行同時測量。基于每個截面需要 3 個位移傳感器進行徑向運動誤差的分離,如果進行在線時時測量,則共需 6 個傳感器。鑒于實驗設備的缺乏,傾角誤差試驗將分兩步進行。
第一步,對兩個截面分別進行三點法頻域誤差分離試驗,如圖 4-4。此步的目的是得到被測試件在各個截面的圓度誤差,同時也能得到主軸在此截面平面內的徑向運動誤差。
第二步,在兩個截面內的 x,y 方向上同時架設 4 個位移傳感器,對主軸的誤差運動進行測量,如圖 4-5,數據處理將在下面的小節中詳細介紹。

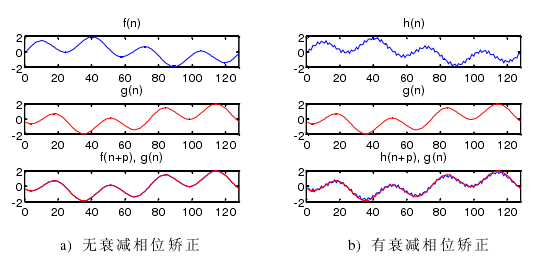
圖 4-6 相位矯正
4.2.2 相同點位非同時測量值的相位矯正
因為傾角運動誤差需要分兩次測量,而且本實驗所用超精密車床的編碼器是增量式而非絕對式的,給實際測量實驗帶來了一定困難。本節將研究傳感器在同一位置的兩次測量值如何保證具有相同的測量起點。
給定一離散周期信號 s(n),從信號 s(n)中兩個不同點位開始分別取一個周期的數據,個數為 N。兩次采樣點序列記為 f(n),g(n),其中 g(n)=f(n+p),其中 p 為兩信號的相移點數。則問題歸化為已知 f(n),g(n),求兩個離散信號序列的相移點數 p。
對 f(n),g(n)做傅里葉變換得


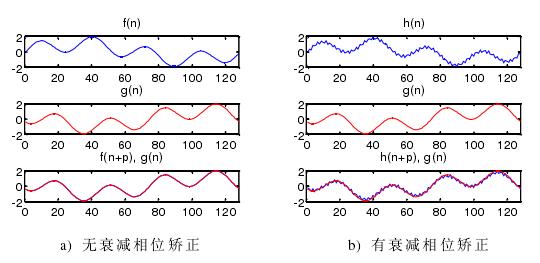
圖 4-6 相位矯正
4.2.3 傾角運動誤差分離實驗數據處理
傾角誤差分離試驗將按兩步進行,首先要到的是被測試件在兩個截面內的圓度誤差。通過對每個截面內三個傳感器采集的數據進行處理,得到被測試件在此截面內的圓度誤差信號。此時需要關注的是被測試件每個點位上實際值,后續雙截面同時處理時要用到這些具體值。
第一步操作如下:
這里不再贅述單截面主軸徑向運動誤差和被測試件的圓度誤差,下面直接給出被測試件兩個截面分別進行三點法誤差分離試驗的數據結果。表 5-1和圖 4-7 給出兩個截面測量數據的最小二乘評價表和實際數據的極坐標圖。
表 5-1 兩截面分別測量得出的圓度誤差和徑向運動誤差

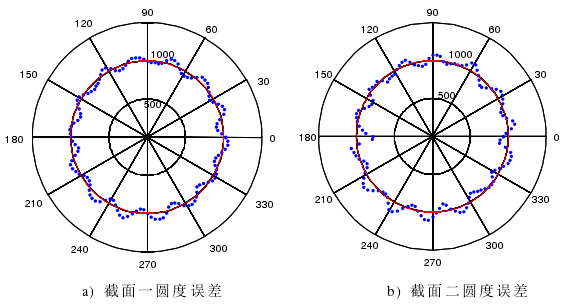
圖 4-7 雙截面分離出的圓度誤差(矯正前)
雖然通過這一步已經分離出主軸在兩個截面內主軸的徑向運動誤差,但是我們不能用這兩個截面在這一步測得的數據來求解主軸傾角運動誤差。原因有二:第一,這兩個截面的三點法頻域誤差分離試驗是分開進行的,也就是說兩截面的徑向運動誤差不是同時得到的;第二,本試驗所采用的超精密車床主軸電機編碼器不是絕對式編碼器,即便不考慮原因一,徑向運動誤差圖也存在相位移動。這些問題將通過第二步來解決。
第二步操作如下:
四個位移傳感器分別安裝在被測試件的兩個截面內 x,y 方向上,對主軸運動進行同時測量。我們已知從每個傳感器采集數據中提取的同步運動誤差信號中只包含被測試件的圓度誤差信號和主軸在此方向上的徑向運動誤差。而經過第一步試驗的處理我們已知被測試件兩截面的圓度誤差值,此時從任何一個傳感器的同步運動誤差信號中減掉被測試件對應點位的圓度誤差值就會得到主軸在此傳感器方向上的徑向運動誤差值。
四個傳感器同時測量可以解決第一步兩截面徑向運動誤差非同時測量的問題,鑒于試驗用超精密車床主軸電機編碼器不是絕對編碼器,另一個需要解決的問題是同一位置處的傳感器的兩次測量數據中相位匹配,此處的相位匹配是指測量點位的匹配對應,用軟件匹配的方法解決硬件編碼器在此次測量試驗中帶來的困難。
主軸電機轉速為 1000 r/min,傳感器采樣頻率設為 25600 Hz。主軸每旋轉一周采樣 1536 點,主軸轉動角度分辨率為 0.2344°,相當于每轉分度 1536線的編碼器。在同一位置處(傳感器的位置,而不是測試件的測點的位置)的傳感器兩次分別測量 20 轉數據,從兩次測量數據中提取的同步運動誤差信號分別記為S1和S2 。因為沒有絕對編碼器,所以每次測量不能保證相同的起始測點。S1 和S2會在相位上出現偏差,如圖 4-8 a),利用算法矯正過的圖形如圖 b)。
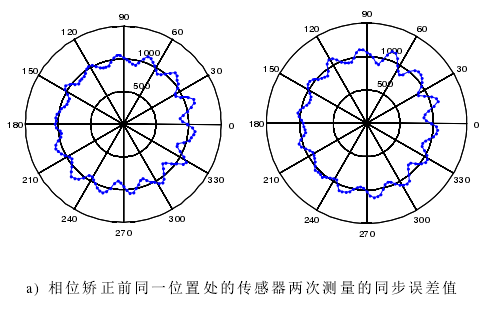
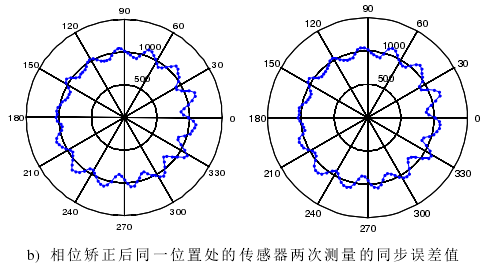
至此,我們已經解決無絕對編碼器帶來的相位捕捉問題。主軸旋轉時對被測試件相同位置處的兩次測量數據經過相位矯正后可以保證測量點位從同一點開始采集。從圖 4-8 b)可以看出相位矯正效果是很好的。
將第一步和第二步傳感器信號進行相位矯正后,從兩個截面 x,y 方向上的傳感器的同步運動誤差中減掉第一步的分離出的圓度誤差即可得到兩個截面的徑向運動誤差,如圖 4-9 所示。
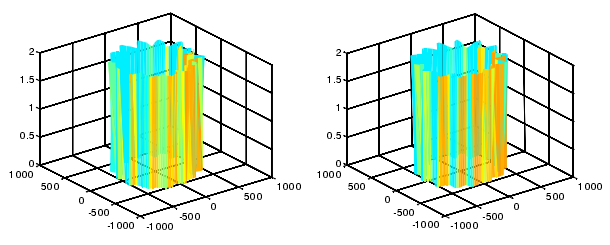
圖 4-9 左側圖為兩截面 x 軸方向運動誤差,右側圖為兩截面 y 軸方向運動誤差
根據公式(4-8),可計算出主軸在 x 軸和 y 軸方向上的傾角運動誤差,如圖 4-10 所示。
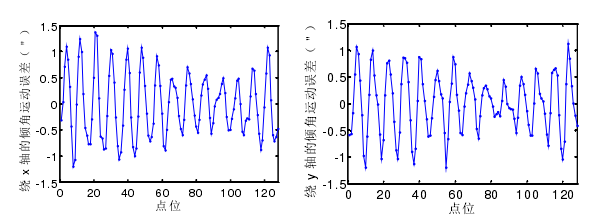
圖 4-10 繞 x 軸和 y 軸的傾角運動誤差
4.2.4 主軸轉速對傾角運動誤差的影響
上節分析的是轉速在 1000 r/min 時,主軸繞 x 軸和 y 軸的傾角運動誤差的分離過程。為研究主軸轉速對傾角運動誤差的影響,試驗還對主軸轉速在600 r/min 和 200 r/min 時進行傾角運動誤差的分離運動,試驗結果如圖 4-11。
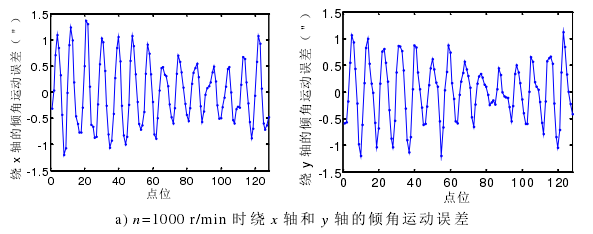
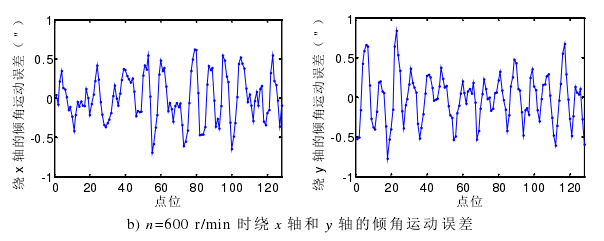
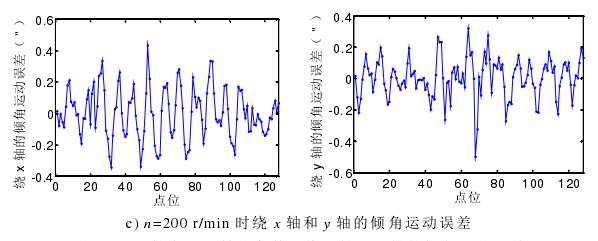
圖 4-11 主軸在不同轉速條件下繞 x 軸和 y 軸的傾角運動誤差
從圖 4-11 可知,隨著主軸轉速的降低,傾角運動誤差隨之減小。綜合之前分析的主軸的徑向回轉運動誤差隨主軸轉速的降低而減小,可知主軸的在 1000 r/min 以內轉動,轉速越低,其轉動穩定性越好。
4.3 本章小結
本章主要分析雙截面測量實驗數據在去掉直流分量后,是處在同一個坐標系——絕對坐標系中的,為傾角運動誤差的計算提供有效數據;在徑向運動誤差的基礎上推導傾角運動誤差求解算法;進行超精密車床主軸傾角運動誤差實際測量實驗,并對不同轉速下主軸傾角誤差運動進行研究。
結論
超精密主軸回轉誤差是影響加工工件表面質量的最主要因素,研究超精密主軸回轉誤差對于評價主軸回轉精度,監測診斷主軸運行故障,預測機床加工工件表面形狀誤差,加工誤差補償及提高機床加工精度等有重要意義。本文以三點法頻域誤差分離技術為基礎,以超精密車床主軸為研究對象,研究主軸的徑向運動誤差和傾角運動誤差的分離。結論如下:
(1)從傳感器測量值實際數學模型的解析構成角度證明最小二乘偏心運動對主軸徑向誤差運動的不可分離性。給出實際測量環境下傳感器安裝角位置偏差和安裝線偏差對誤差分離精度的定量分析,為超精密車床主軸回轉誤差納米級測量采集數據的可靠性提高理論保證。
(2)在頻域中對除噪、濾波、同步運動誤差的提取以及三點法算法的前半部分進行連續性處理,減少測量信號在時域頻域中的變換計算。從超精密車床加工工件表面成形角度分析去除一階諧波分量的依據。
(3)實際測出超精密車床主軸徑向運動誤差,并根據推導出的主軸傾角運動誤差分離算法,測得超精密車床主軸傾角誤差。
本文搭建的超精密車床主軸回轉誤差測試系統還存在一定的問題。雖然摒棄了安裝標準件到主軸上進行測量的方案,采用超精密車床自身加工高精度測試件在無拆卸狀態下直接進行測量,依然不能很好地解決最小二乘偏心運動對主軸回轉誤差的影響。在今后的工作中,將重點解決一下幾個問題:
(1)主軸徑向運動誤差的一階諧波分量與被測截面最小二乘偏心運動量的分離。一階諧波分量的分離同樣影響到傾角運動誤差的分離,所以此問題需待解決。
(2)主軸回轉誤差是影響超精密車床加工對稱回轉體和快刀加工非對稱回轉體的表面質量最主要的因素,所以回轉誤差的加工補償也是后續工作的重點。
投稿箱:
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
更多本專題新聞
專題點擊前十
| 更多










