車削用電主軸永磁同步電機電磁與熱特性的研究(中)
2017-2-10 來源:沈陽工業大學 作者:閆佳寧
3.1 車削用電主軸永磁同步電機的弱磁問題
3.1.1 永磁電機弱磁原理
電勵磁同步電動機可以通過調節勵磁電流增大其恒功率運行范圍,而永磁同步電機是由永磁材料提供勵磁,磁場恒定,勵磁強度不可調節,轉子磁場在定子電樞繞組內感應的反電動勢與電機轉速成正比,當電機端電壓隨轉速升高到變頻器能夠輸出的最高電壓之后,電機的轉速會受到限制,若要繼續升高電機轉速則需要對氣隙磁通進行削弱,即需要對電機進行弱磁控制以維持反電動勢的平衡,擴大電機的速度范圍,此時電機將不再做恒轉矩運行。


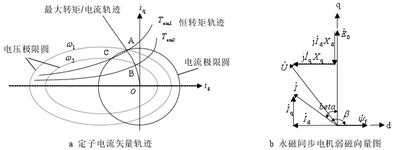
圖 3.1 弱磁控制原理圖


3.2 車削用電主軸永磁同步電機的弱磁計算分析
3.2.1 弱磁磁路特性分析
對電機模型進行靜態場仿真分析,考察當不注入弱磁電流,額定電流 50A 加載在交直軸不同位置時,電機的空載磁場、直軸電樞反應磁場、交軸電樞反應磁場、某負載磁場四種情況下的磁場分布,旨在比較不同情況下的磁場特點并得出結論,為弱磁下的轉速分析做鋪墊。

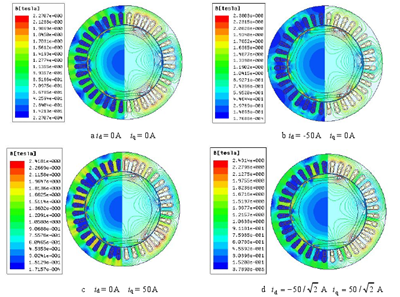
圖 3.2 不同情況下磁場分布
比較圖 3.2 a 和 b 發現,當電流分量全部加載在直軸上,id 為負時,電機齒部和軛部磁密減小明顯,處于去磁狀態;比較 a 和 c 發現,當電流分量全部加載在交軸上時,c 中磁力線較 a 發生了畸變,這說明 iq 的作用為使磁力線產生畸變;a、b、c 的比較表明,電機運行過程中定子電流的交直軸分量不斷變化,使 d、q 軸之間存在交叉飽和影響,這會給 Ld 的計算帶來困難。此外永磁體不同的放置方式和磁極形狀的靈活多變,也使電機的交、直軸電感參數與電流的關系呈現出非線性[46,47]。所以,要準確分析永磁同步電動機弱磁擴速的性能,在計算電機參數時就要充分考慮交叉飽和和非線性的影響,采用場的方法研究電機的電感參數便非常必要。
3.2.2 基于有限元的交直軸電感參數計算
傳統的等效磁路法計算電感需要改變轉子位置,求得定子各相繞組的自感和互感隨轉子磁路變化的關系,對于不同的永磁體放置方式,還需進行修正,計算過程相對復雜,如果修正系數選擇不當還將影響計算的準確性[48]。Maxwell 靜態場法對電機的電感矩陣的仿真計算是基于特定激勵且針對完整閉合繞組,因此需要在設置前確定 6 極 36 槽電主軸電機的每個繞組的回路關系及匝數Turns,完成電感矩陣 Matrix 的設置。各繞組回路連接后再將屬于同一相的繞組歸為一組,并設置并聯支路數 Branches。然后設置不同的 id 和 iq 求得不同情況下的三相電感值 LABC,通過變換即可求得 d、q 軸電感值,具體做法如下。

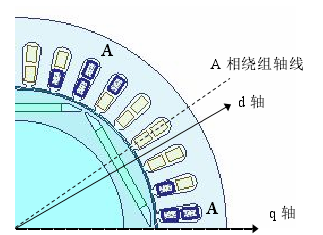
圖 3.3 初始時刻位置示意圖





圖 3.4 id 對電感影響
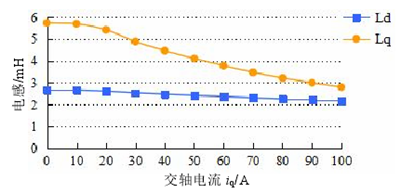
圖 3.5 iq 對電感影響

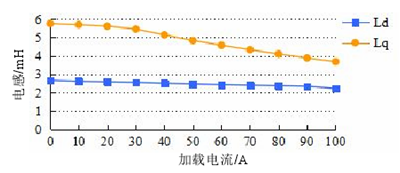
圖 3.6 id 與 iq 對電感影響
從上面的分析看,無論是單獨施加 id 分量還是 iq 分量,Ld 均變化不大,但 Lq 的反應很敏感。在電機的實際控制中,根據最大轉矩與電流比的矢量控制方式,交直軸電流是同時存在的,所以在分析時要考慮到交直軸電感之間的耦合問題。
3.2.3 弱磁控制下的速度校核
根據上面分析闡述,本課題所用電主軸電機在達到轉速拐點之后采用弱磁控制,弱磁時能達到的最大電流為 100A,由上文分析可知,當電流全部位于直軸時,電機能達到此種控制下的最高轉速,現對其理想狀態下的弱磁最大速度進行分析。當 id= -100A,iq= 0A 即電流分量全部為直軸分量時,在靜態場中計算得到三相電感矩陣為
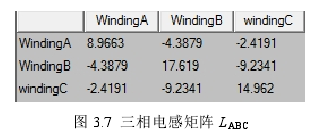

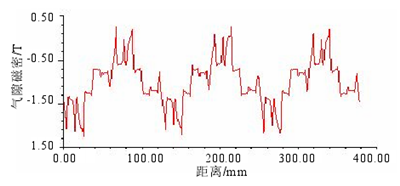
圖 3.8 弱磁時徑向氣隙磁密

300Hz,并帶有待確定控制角 beta 的電流源,對 beta 進行參數化,以找到合適的角度使得電機輸出能夠達到二倍弱磁速度時所對應的轉矩。當 beta 在 0°~90°之間、以 10°為步長時,輸出的轉矩如圖 3.9 所示。若能達到二倍弱磁速度則電機輸出的轉矩應該為 44.6N?m 左右,從圖中可以看出當 beta 在 80°~90°之間時平均轉矩為-0.0514N?m~54.5645N?m,涵蓋了目標轉矩,則將 beta 定位于 80°~85°度繼續細分進行參數化,發現當 beta=81.8°時對應的輸出轉矩為 44.85N?m,即尋找到了合適的控制角 beta 使電機輸出二倍弱磁速度對應的轉矩,說明電機能夠達到二倍弱磁速度,此時的控制角為 81.8°。圖 3.10 為控制角 beta 與轉速的關系。
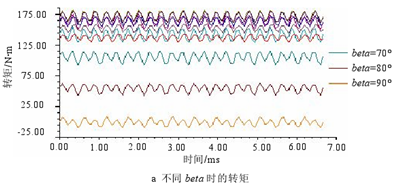
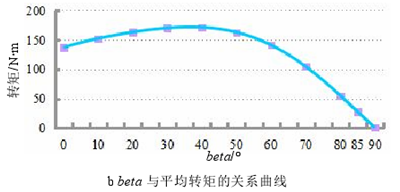
圖 3.9 不同 beta 對應的轉矩
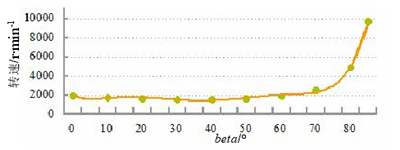
圖 3.10 不同 beta 與轉速的關系
從圖 3.10 中可看出當控制角超過 70°后轉速有所上升,在輸出結果中得到當控制角為 81.8°時轉速可達到 6000r/min,可以滿足滿足車削加工中二倍調速的需求。
3.3 車削用電主軸永磁同步電機的損耗計算
3.3.1 損耗計算方法
(1)鐵耗計算
1)傳統鐵耗計算模型
電機鐵耗包括基本鐵耗和空載鐵心附加損耗,基本鐵耗又包括磁滯損耗和渦流損耗。傳統計算方法是將鐵心的磁滯損耗和渦流損耗以總和的形式計算,計算公式為

電機運行時旋轉磁化主要發生在軛部,交變磁化主要發生在齒部,二者性質不同,需要將軛部損耗和齒部損耗分別計算,所取 B 為軛部磁路磁通密度最大值,齒部磁路磁通密度平均值。齒部與軛部
ak 的取值也有所不同,但都是將磁通密度分布不均勻、磁通密度隨時間不按正弦變化(即諧波磁場產生的附加鐵耗)、機械加工等多種因素考慮在內的經驗系數。對于空載鐵心附加損耗通常不做詳細計算,而是根據不同類別不同容量規定其為輸入功率一定的百分比。在工廠計算中則是通過取更高的 ka 來計及空載鐵心附加損耗的影響。由此可見,電機傳統鐵耗計算模型雖然使用起來簡便實用,但往往依賴于經驗系數的取值,在車削電主軸電機設計研發初期不適宜采用。
2)基于有限元法的 Bertotti 鐵耗分離計算模型
目前利用有限元法計算電機鐵耗所采用最多的模型為 Bertotti 鐵耗分離模型,上述提到傳統方法中計及磁密不均、磁密非正弦變化、機械加工影響硅鋼片導磁性能等多種因素對損耗結果的影響是通過引入經驗系數實現的,而有限元法可通過對得到的鐵心內部任意區域的磁密或計算模型的處理計及上述因素。Bertotti 鐵耗分離計算模型由 Bertotti 于 1988 年提出,是根據損耗的不同產生機理將其分別加以計算,因而得名鐵耗分離計算模型。在正弦磁通下,由磁滯、渦流及附加損耗組成的三項式鐵損模型可表示為[49-51]





3.3.2 額定與弱磁時的損耗比較分析
(1)定子鐵耗的有限元計算
目前大多數文獻采用有限元法計算鐵耗時都采用 2D 計算,其精度已經能夠滿足要求,且 3D 計算占用資源過大,沒有必要采用。在計算定子鐵心損耗前,首先要確定鐵心損耗系數,本課題所設計樣機定、轉子均選用 DW310_35 型號硅鋼片材料,其 50Hz、60Hz、100Hz、200Hz、400Hz、1000Hz頻 率 下 的 B-P 曲 線 及 擬 合 曲 線 如 圖 3.11 所 示 。 擬 合 后 得 到 損 耗 系 數 值 為 :
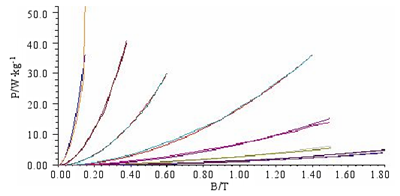
圖 3.11 硅鋼片材料 B-P 曲線
對第 2 章所設計的 6 極 36 槽車削電主軸電機模型的軛部和齒部進行分割(分割線與槽底有適當距離),在額定轉速 3000r/min、額定電壓運行情況下進行時步有限元仿真,分別得到定子軛部和齒部的鐵心損耗,計算結果如圖 3.12 所示。圖 3.13 為弱磁條件下損耗的計算結果。
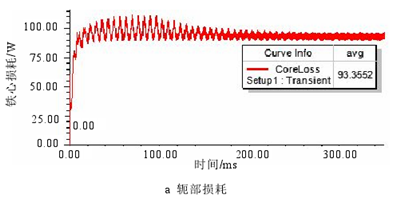
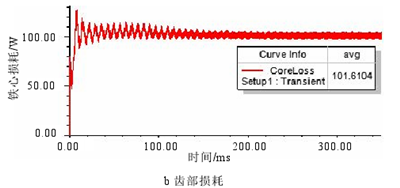
圖 3.12 額定時定子鐵心損耗
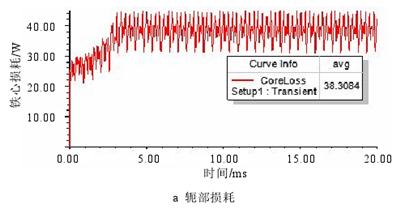
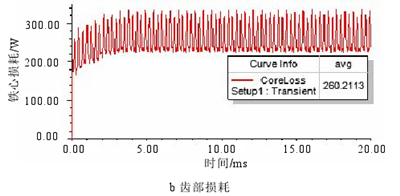
圖 3.13 弱磁時定子鐵心損耗
當轉速 6000r/min,電流有效值 100A 弱磁時,從圖 3.13 中可以看出在鐵耗平均值穩定后幅值變化較大,這是因為弱磁控制時諧波增大造成的。且對比額定時的鐵耗可以發現,軛部鐵耗減小,齒部鐵耗增大,與磁密分析的結果一致。此外,弱磁時的總損耗也較額定時有所增大。
(2)雜散損耗的計算
電機損耗包括四類:鐵耗、銅耗、機械損耗和雜散損耗。前三種損耗的計算方法在上文已經有所闡述,對于本課題所研究的車削電主軸電機,雜散損耗以轉子鐵心損耗和永磁體渦流損耗計。額定和弱磁時經有限計算得到的轉子鐵心損耗和永磁體渦流損耗如圖 3.14 和圖 3.15 所示。可以看出,額定甚至在弱磁運行時轉子鐵心損耗和永磁體渦流損耗都不大,額定時轉子鐵心損耗和永磁體渦流損耗分別占額定功率的 0.03%、0.01%,弱磁時兩者分別占額定功率的 0.14%、0.01%。綜合以上分析計算,將損耗結果在柱狀圖 3.16 中進行表示。
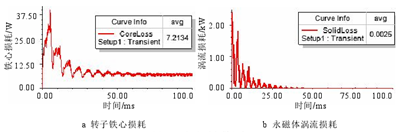
圖 3.14 額定時雜散損耗
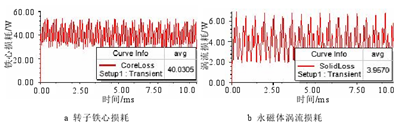
圖 3.15 弱磁時雜散損耗
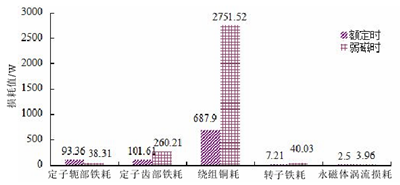
圖 3.16 額定與弱磁時的損耗對比圖
從圖 3.16 中可以直觀看出二倍弱磁速度時定子軛部鐵耗減小了 59.0%,定子齒部鐵耗增大了 156.1%,繞組銅耗增大了 300.0%,轉子鐵耗增大了 456.7%,永磁體渦流損耗增大了 58.4%,但轉子鐵耗和永磁體渦流損耗其值本身很小,對于功率不大、非高頻的永磁電機若不做特殊研究需求,對于總損耗的影響可以忽略不計。
3.4 本章小結
本章比較系統的對車削用電主軸的弱磁問題和損耗計算進行了闡述分析,總結如下。
(1)從弱磁原理出發,分析了提高電機弱磁速度的方法,并對交軸電樞反應和直軸電樞反應時的磁路特性進行分析,發現 d、q 軸之間的磁路存在交叉飽和影響,直軸電流 id 的作用是使磁路去磁,交軸電流 iq 的作用為使磁力線產生畸變;隨后基于場計算得到隨 id 與 iq 增大,直軸電感 Ld 和交軸電感 Lq 都有所下降,但 Ld 隨電流變化不大,L
q 對電流變化表現得很敏感;通過場計算得到此未經特殊設計的電機 Ld 的值為3.32m H,進而通過解析公式計算出所設計電機在電流全部在直軸上時,能達到的最高轉速為 6936.4r/min 后,采用有限元計算進行驗證,找到當 ilim=100A,控制角 beta=81.8°時,能夠達到所需二倍弱磁速度 6000r/min。
(2)介紹了電機鐵耗,銅耗,機械損耗以及雜散損耗的計算方法,并基于有限元求得了電機的額定時的定子鐵耗約為 195.0W,弱磁時約為 298.5W,增加了 53.1%;額定時銅耗約 687.9W,弱磁時因電流為額定的二倍,銅耗變為原來四倍;額定時轉子鐵耗約 7.2W,弱磁時約 40.0W,增加了 455.5%;額定時永磁體渦流損耗約為 2.5W,弱磁時約為 3.96W,增加了 58.4%。此外,雜散損耗為轉子鐵耗和永磁體渦流損耗,其值與其它損耗相比很小。
第 4 章 20k W 水冷樣機的溫升計算與實驗對比
電機穩定運行一段時間后溫度也趨于穩定,其穩態溫升和溫度最高點直接影響電機的運行可靠性和使用壽命,溫升過高會引起絕緣老化、永磁體退磁,準確計算電機的溫度場分布規律對電機冷卻系統的設計、降低電機溫升、合理選取絕緣材料都具有重要意義。
本章對一臺 20k W 水冷樣機進行溫度場仿真計算,然后將計算結果與其實驗數據做對比,從而驗證本章計算方法對于此類電機溫度場計算的準確性,其中包括建模簡化時繞組的等效方法、導熱系數的選取、熱源加載、裝配間隙等關鍵步驟的處理。
4.1 溫度場計算的數學模型
電機內定子鐵心、繞組、軸承等部件的發熱情況不盡相同,便引起了熱量的傳遞,盡管熱量傳播的過程十分復雜,但一般總先由發熱體內部借傳導作用傳到發熱體表面,然后在通過對流和輻射作用散到周圍介質中,傳遞時不僅需要滿足能量守恒、動量守恒和質量守恒定律,還要滿足熱傳導方程。根據傳熱學的基本理論,在直角坐標系下,電機內的穩態溫度場求解可歸結為如下邊界問題[52]。

4.2 20k W 水冷樣機熱計算的前處理
20k W 水冷永磁同步牽引電機的基本參數見表 4.1。本課題溫度場的計算是基于有限體積法,用 Solidworks 建立電機的三維模型時為方便求解域的建立,應對模型做適當簡化(確保不改變物理過程),否則剖分質量難以達到計算要求,會給溫度場分析帶來不便。
表 4.1 20k W 樣機基本參數表
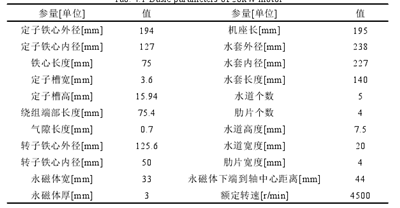
4.2.1 三維求解域的建模與簡化
(1)轉子鐵心的簡化建模
如第 3 章所闡述,樣機中的實心塊狀永磁體存在渦流損耗,硅鋼片疊壓的轉子鐵心存在鐵心損耗,兩者即是熱源又是導熱媒介,建模時應盡可能接近實際模型。內置“V 一”型永磁體結構較為復雜,端部存在不規則形狀的窄尖隔磁橋,建模時進行如圖 4.1 所示的簡化,這樣處理既能提高部分質量,又能盡可能的接近實際情況。
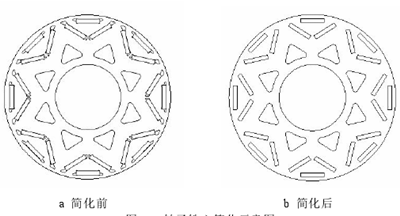
圖 4.1 轉子鐵心簡化示意圖
(2)槽內所有絕緣和繞組端部建模的簡化方法電機定子槽內絕緣組成復雜,有繞組股線絕緣(絕緣漆膜)、槽絕緣和層間絕緣、浸漬漆,建模和剖分時無法完全考慮,因而通過如下假設將其化為等效槽絕緣。
1)銅線的絕緣漆分布均勻;
2)槽絕緣和層間絕緣填充均勻;
3)電機浸漆狀態良好,浸漬漆填充均勻;
4)槽內絕緣與定子鐵心及繞組緊密接觸。其厚度計算方法如流程圖 4.2 所示。
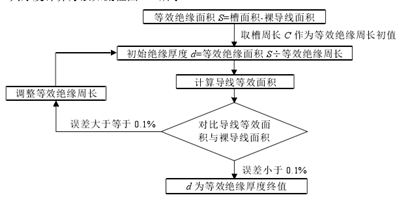
圖 4.2 等效槽絕緣厚度計算方法
對于雙層繞組,在計算導線等效面積時注意保證上下層導線面積相等且等效槽絕緣厚度均為 d。經計算,樣機的等效絕緣厚度為 1.21mm,其示意圖如圖 4.3 所示。
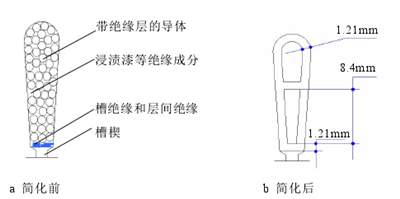
圖 4.3 槽內繞組及絕緣的等效模型
此外,繞組端部采用直線來等效其實際排布,因為物體的溫升與其散熱面積、散熱系數、熱流密度以及周圍環境有關,而與物體形狀無關。
(3)端蓋、轉軸等其余部件的簡化建模
端蓋和轉軸自身不產生熱量,僅作為導熱媒介,且電機大部分熱量由機殼與水套中所流通的冷卻水帶走,所以為提高剖分質量,將端蓋圓倒角簡化為直角,僅保留轉軸與端蓋、轉子、軸承接觸部位的臺階。
此外,將電機固定所用的緊固螺釘、扣片與其相接觸部件融合為一體。在定子鐵心端部有定子絕緣端板,轉子鐵心端部有轉子壓板,它們所用材料的導熱系數與端部靜止的空氣非常接近,故將定子絕緣端板和轉子壓板省略按空氣處理。鑒于本臺電機是圓周對稱結構,又考慮到計算機配置和計算時間等問題,按上述處理后建立電機的 1/8 模型如圖 4.4 所示。

圖 4.4 20k W 水冷樣機三維溫度場的求解模型
4.2.2 求解模型的剖分與邊界條件
(1)模型的剖分
流體與溫度場計算中,網格剖分關系著計算的收斂性和結果的準確性,可以說占據了流體與溫度計算百分之七十的工作量。剖分時六面體網格與四面體網格相比具有顯著優勢:六面體網格更能迎合流場方向(如邊界層處),離散誤差小;剖分同樣網格尺寸時數量少,計算時間短。此外,結構化網格網格點之間的鄰近關系有序且規則,計算效率比非結構化網格高,故在進行對網格質量要求比較高的流體與溫度場計算時,盡量剖分為結構化六面體網格。
電機內部氣體分布極其不規則,為提高剖分質量,有時需要切分為規則整塊進行剖分。對于出現圓弧的部件,可以先對面進行四面體剖分,再用掃掠剖分為六面體。此外,流體場變化大的地方需要細剖比如氣隙等,流體場變化小的地方可以適當粗剖,比如端蓋等,在不影響計算精度的情況下,合理布置網格,是提高網格劃分質量的關鍵。但剖分尺寸不宜相差過大,網格越均勻,計算越容易收斂。在前處理軟件 Gambit中剖分后,電機各部位的剖分尺寸如表 4.2 所示。
表 4.2 20k W 樣機各部位剖分尺寸表
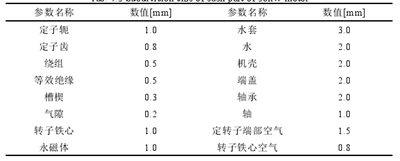
圖 4.5 為網格質量 Equisize Skew 的檢查結果,對各部件單獨檢查發現只有槽楔和軸的失真度較大為 0.68,其余部分失真度比其更小,剖分效果理想,整機剖分結果和氣隙剖分結果如圖 4.6 所示。
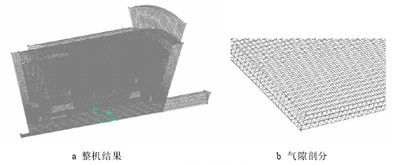
圖 4.6 20k W 水冷電機剖分結果
(2)模型的邊界條件
根據電機系統結構特點以及整域傳熱特性,求解域內具體邊界條件設置為:
1)將 1/8 模型的切面設置為絕熱 WALL 邊界;
2)電機外表面設置為絕熱 WALL 邊界;
3)其余互相接觸且外圈輪廓形狀一致的一對面設置為 INTERFACE 耦合邊界。要注意設置耦合面的正確性,否則將得到錯誤的溫度分布。
4.2.3 各部位傳熱系數的確定
電機內部的熱傳遞主要靠熱傳導方式實現,不同材料的部件傳遞熱量的能力也不同,傳熱系數的準確確定是溫度場計算的前提條件。樣機中部分導熱系數依據材料的固有屬性確定,部分傳熱系數需要根據等效方法進行相應計算。
(1)氣隙等效傳熱系數的計算
轉子旋轉使氣隙內空氣對定轉子交換熱量的能力強于靜止狀態。引入有效傳熱系數λeff 來描述氣隙中流動空氣的熱交換能力,即單位時間內靜止流體在定轉子之間所傳遞的熱量和流動空氣所傳遞的熱量相等,這樣可把旋轉的轉子視為靜止不動處理[54,55]。根據文獻[55],假設定子內表面和轉子外表面為光滑圓柱面,則氣隙中的雷諾數為

(2)定轉子鐵心疊片等效傳熱系數的計算
樣機的定轉子鐵心由硅鋼片沿軸向疊壓而成,由于工藝限制,片與片之間不能緊密貼合,導致疊片之間存有空氣,且鐵心疊片在加工過程中會對鐵心進行浸漆,使其傳熱系數遠小于純硅鋼片的導熱系數,這也導致了鐵心疊片在 x 方向、y 方向、z 方向傳熱的各向異性。為此,本課題采用軸向等效傳熱系數計及硅鋼片漆和空氣對鐵心疊片的影響。由相關文獻知,定子鐵心軸向等效傳熱系數的計算式為

(3)等效槽絕緣傳熱系數的計算
定子槽內絕緣組成比較復雜,含有導線漆、浸漬漆、槽絕緣材料,為了便于計算等效槽絕緣的傳熱系數,做如下假設:
1)忽略股線間由于絕緣漆膜存在造成的溫差;
2)認為定子槽內繞組的發熱均勻,忽略繞組的集膚效應。
按照 4.2.1 中的方法將定子槽內的絕緣等效成一個實體后,其等效傳熱系數可以由公式(4.7)確定。

(4)各實體材料的導熱系數
以上計算得到的氣隙等效傳熱系數、定轉子鐵心疊片等效傳熱系數、等效槽絕緣的傳熱系數,同樣機內其余各部件所采用的材料及其導熱系數羅列在表 4.3 中,數據來源于《Y2 系列三相異步電機技術手冊》和魏永田的《電機內熱交換》。表中數據為考慮定轉子鐵心疊片的各向異性,氣隙、等效槽絕緣、繞組、空氣、軸承等介質的各向同性的數據。此外,對于封閉式電機,繞組端部可以當做自然散熱處理,取高溫空氣的導熱系數進行計算。
表 4.3 20k W 電機各部分材料及傳熱系數
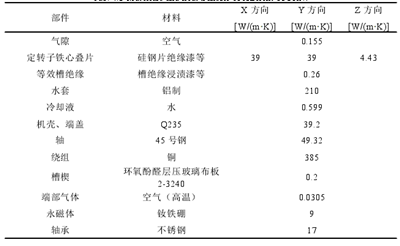
(5)機殼表面散熱系數的處理
依據《電機內熱交換》,考慮樣機內有氣體循環,用式(4.8)計算機殼表面散熱系數。

4.2.4 裝配間隙的處理
電機部件間存在裝配間隙,如機殼與定子間、轉子與永磁體間、轉子與軸間、端蓋與軸承間、端蓋與機座間、端蓋與軸間。裝配間隙相當于靜止的薄空氣,其導熱系數遠不及實體材料,故對電機的最高溫升影響很大,在電機溫度場計算中需予以考慮。建模時無需把裝配間隙建成實體,只需在 Fluent 中找到相應部位的裝配間隙,并設置厚度和導熱系數。機殼與定子間的裝配間隙用公式(4.9)計算。
計算得到定子鐵心與機座的裝配間隙為 0.0000113m。此間隙的空氣溫度僅略大于環境溫度,取低溫下空氣導熱系數,為 0.0242W/(m.K)。而轉子鐵心與永磁體的裝配間隙為 0.0001m(工藝引起,根據公差帶相減平均而得)。轉子鐵心與永磁體間隙溫度較高,取高溫空氣的導熱系數 0.0305W/(m.K)。其余部分類似,得到表 4.4[56]。
表 4.4 裝配間隙明細表
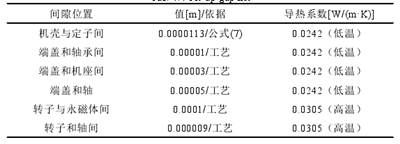
4.3 20k W 水冷樣機的穩態溫度場計算
4.3.1 求解初始條件
(1)給定環境溫度為 27℃(300K)。
(2)給定速度入口 VELCITY_INLET,水速為 1.975m/s(即實驗水速)。
(3)給定壓力出口 PRESSURE_OUTLET,零相對壓力,即一個標準大氣壓,101325Pa。
(4)水力直徑若為圓形管道,則水力直徑 D 為圓形管道直徑,若流體流動的界面為其它形狀,那么可由下式求得等效水力直徑 DH
其中,A 為管道截面積,U 為流體濕周。計算得到 20k W 樣機的水力直徑為 10.91mm。
(5)湍流強度
管道內流體與機殼和水套之間的換熱屬于強迫對流換熱,流體的雷諾數可由下式得到

其中,lu 為流體的特征速度 1.975m/s,fv 為流體的運動黏度。
則求得冷卻水的雷諾數為 26987.6。當流體的雷諾數在 2300~10000 之間時,流體處于層流向湍流過渡狀態,大于 10000 時流體處于湍流狀態,則樣機通入的冷卻水為湍流流動,其湍流強度 I 可由下式確定

計算得到湍流強度為 4.5%。
4.3.2 樣機熱源分布
溫度場求解時有單向耦合和雙向耦合兩種方法。將電磁場計算中各部件的損耗結果作為溫度場的熱源,而兩場分別進行計算,即為單向耦合方法。雙向耦合是通過電磁場分析和溫度場相互傳遞數據進行迭代,這種方法運用起來比較困難,也耗費時間。兩種方法如圖 4.7 所示。目前幾乎所有的電機熱分析都采用單向耦合,本課題也是。
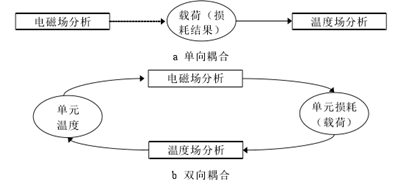
圖 4.7 溫度場計算方法

表 4.5 實測損耗值(環境溫度 27℃)

按表 4.5 的比例進行分配,由式計算可得樣機各部位的生熱率如表 4.6 所示,其它部位的生熱率為零。
表 4.6 各部位生熱率
4.3.3 溫度場計算結果與實驗對比分析
經過前述簡化建模、網格剖分等過程后,利用 Workbench 中的 Fluent 模塊對樣機進行穩態熱分析,經過樣機材料參數定義、邊界條件設置、加載熱源等步驟,在收斂達到要求精度后,迭代求解自動停止,得到電機的溫度場分布如圖 4.8 所示。
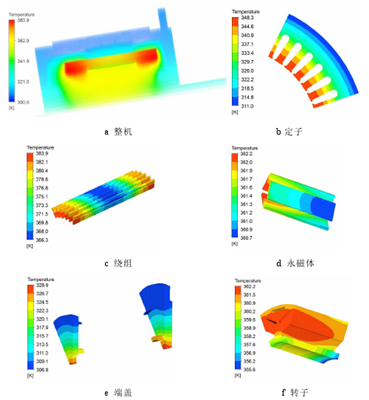
圖 4.8 20k W 電機溫度分布圖
從圖 4.8 a 中,可以看出樣機的最高溫升為 83.9K,且高溫部分主要集中在繞組、轉子鐵心和永磁體處,機殼表面溫升最低。圖 b 中定子鐵心最高溫升為 48.3K,最低溫升為 11K,出現了較大的溫度梯度,定子齒部的溫升相對軛部要高,和槽口接觸的部分散熱相對最差,靠近機殼和冷卻水處的溫度迅速降低,說明水的流動起到了良好的散熱效果。圖 c 中所示繞組中部散熱較好而端部散熱較差,最高溫升 83.9K,也是樣機的最高溫升,并且集中在下層繞組,這是由于繞組端部由空氣散熱,空氣的導熱能力較差遠不如硅鋼片,熱量傳遞較少。圖 d 中所示永磁體最高溫升為 62.2K,最低溫升60.7K,該“V 一”結構的永磁體“一”型部分溫度較低,結合圖 f 可知,其熱量主要熱量由轉子上部和氣隙傳遞出去。圖 e 中所示端蓋的最高溫升為 28.9K,最低溫升為6.9K,端蓋的最熱點出現在與軸承及轉軸接觸的位置。從上述結果可以看出,由有限體積法計算得到的樣機各部分溫度都在溫升限度范圍內,通過埋熱電偶實驗測得的溫升及計算結果對比如表 4.7 所示。
表 4.7 仿真與實驗對比結果
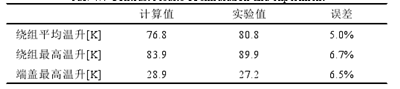
通過實驗值與計算值的對比可知,該方法的誤差均在允許范圍內;端蓋的溫度分布規律與實驗相符,最熱點位置相同,驗證了本章基于有限體積的溫度場分析方法能夠滿足工程計算需要。
4.4 本章小結
本章以一臺 20k W 水冷永磁同步樣機為例,確定了電機的建模等效方法,包括轉子鐵心的簡化建模、槽內所有絕緣和繞組端部建模的簡化方法、端蓋轉軸等其余部件的簡化建模,介紹了剖分的注意事項和技巧,邊界條件的確立,氣隙、定轉子鐵心疊片、等效槽絕緣傳熱系數、機殼表面散熱系數的計算方法,以及裝配間隙的處理等,最后用 Fluent 軟件計算了電機溫度場分布,與實驗值進行對比,得到結論如下:
(1)由有限體積法得到的樣機最高溫升為 83.9K,與實驗值 89.9K 的誤差為 6.7%;繞組平均溫升為 76.8K,與實驗值 80.8K 的誤差為 5%;端蓋最高溫升 28.9K 與實驗值27.2K 誤差 6.5%,驗證了溫度場計算方法的準確性。
(2)該樣機的溫升最高點位于繞組端部下層繞組處;繞組、轉子、永磁體溫度較高,冷卻水有效通過機殼帶走熱量,溫度梯度降落趨勢合理。
投稿箱:
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
更多本專題新聞
專題點擊前十
| 更多










