試論車刀幾何參數對數控車床加工精度的影響
2018-5-14 來源: 四川職業技術學院 作者:李進東 吳國明
【摘 要】隨著工業技術的發展,數控車床在工業加工中的應用越來越廣泛。數控加工過程中,一般對刀具刀尖的圓弧半徑 r、主偏角 kr、刀尖距離零件中心高的偏差尺寸等幾何參數進行重點探究,以提高工件表面的光滑程度、減緩刀具磨損,便于對刀具的切削力進行控制。刀具幾何參數對加工零件的軸向尺寸誤差和縱向尺寸誤差產生影響,加工零件的表面形狀也會出現變化。本文重點探究了數控車床刀具刀尖圓弧半徑對零件加工精度的影響,便于零件加工過程中采取有效的措施。
【關鍵詞】刀具 幾何參數 零件加工 精度影響
數控車床加工過程中,零件的質量會受到多種因素的影響,例如車刀刀具刀尖圓弧半徑、主偏角等幾何參數,刀具使用過程中幾何參數將會出現變化,影響零件的加工質量、尺寸精度和形狀精度,加快刀具的磨損程度。因此在零件加工的過程中,必須結合實際零件的尺寸,合理選擇刀具刀尖的圓弧半徑,應用有效的方法提高零件的加工精度和加工質量。
1 、刀尖圓弧半徑影響圓柱類零件尺寸精度
車刀與被加工零件表面的接觸切點運動形成完整的表面,圖1 是幾種常見的零件加工方式。
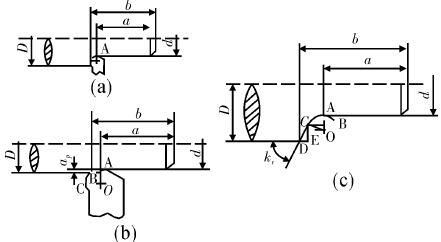
圖 1 典型零件加工方式
圖中 A 為刀尖圓弧頂點,當主偏角 kr= 90° 時,刀尖圓弧頂點A 可以滿足被加工零件軸向尺寸的精度要求。如( a) 所示,如果( D - d) /2 = ap> r,加工過程中刀尖圓弧半徑將會導致被加工零件的軸向尺寸出現變化,將變化量記為△a,則△a = b - a = r,其中 a 表示刀具的實際軸向位移尺寸,b 表示被加工零件的軸向尺寸,r 表示車刀刀具刀尖的圓弧半徑。
此時的 a即為刀具實際軸向位移尺寸,其值為 a = b - △a = b - r。

圖中 A 為刀尖圓弧頂點,當主偏角 kr= 90° 時,刀尖圓弧頂點A 可以滿足被加工零件軸向尺寸的精度要求。如( a) 所示,如果( D - d) /2 = ap> r,加工過程中刀尖圓弧半徑將會導致被加工零件的軸向尺寸出現變化,將變化量記為△a,則△a = b - a = r,其中 a 表示刀具的實際軸向位移尺寸,b 表示被加工零件的軸向尺寸,r 表示車刀刀具刀尖的圓弧半徑。此時的 a即為刀具實際軸向位移尺寸,其值為 a = b - △a = b - r。
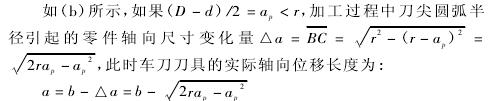

如果( D - d) /2 = ap< r,刀尖的圓弧部分將承擔全部的切削力,軸向尺寸變化量△a 和車刀刀具的實際位移長度 a 和前述計算方法相同。總之,在加工圓柱類零件的過程中,車刀刀具刀尖圓弧半徑和車刀的主偏角將會對被加工零件的軸向尺寸產生較大的影響,在刀尖圓弧半徑不斷增大的過程中,軸向尺寸的變化量也會越大,反之亦然。
因此在編制零件加工程序的同時,必須注重軸向位移尺寸的改變,但是刀尖圓弧半徑和主偏角對圓柱類零件的徑向尺寸精度不會產生影響。2 刀尖圓弧半徑影響單段錐體類零件尺寸精度圖 2 是單段錐體類零件的加工示意圖。

圖 2 單段錐體類零件的加工示意
加工單段錐體類零件的過程中,如果車刀刀具位于初始加工店,即Ⅰ位置時,刀尖圓弧上的 B'點將與椎體類零件的小端起點相切。軟件編程時也會以車刀刀具刀尖圓弧的中心點為基準,將錐體類零件小端部分的軸向尺寸變化量記為。零件加工結束后,車刀將會停止在Ⅱ位置,刀具刀尖圓弧半徑與錐體類零件相切于B 點。因此,如果刀具的實際位移寸為 a,椎體類零件的軸向長

因此,在加工單段錐體類零件的過程中,必須重點考慮車刀刀尖圓環半徑的尺寸影響,在椎體軸向尺寸、徑向尺寸發生變化的過程中,刀尖圓弧半徑增大,被加工零件的軸向尺寸也會增大,而徑向尺寸減小,刀尖圓弧半徑減小,被加工零件的軸向尺寸減小,徑向尺寸增大; 椎體零件的錐角增大,軸向尺寸的變化量增大,徑向尺寸減小,椎體零件的錐角減小,軸向尺寸減小,徑向尺寸增大。
3 、刀尖圓弧半徑影響雙段外錐面零件表面尺寸
加工雙段外錐面零件的過程中,車刀刀具和零件的相對位置如圖 3 所示。
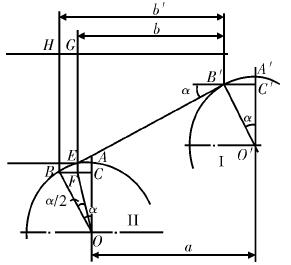
圖 3 雙段外錐面零件加工
如果刀具位于初始加工位置,此時可以看作單椎體零件加工,軸向尺寸的變化與前述類似,如果刀具位于圖 3 位置,處于第一段單段椎體加工的結束階段,也位于第二段椎體的初始加工位置。這種情況下的刀尖圓弧和第一段單段椎體零件和第二段椎體零件分別相切于點 B 和點 E。圖中 DBLEF 即為理論要求軌跡,被加工零件受到圓弧半徑尺寸的影響,實際軌跡會變化為 DBL'EF,其中圓弧主要由車刀刀具刀尖圓弧形成。
在刀尖圓弧半徑的影響下,被加工兩段椎體零件的軸向尺寸和徑向尺寸都會受到影響,其中第一段椎體的軸向尺寸變化量△a1= b1- a1= LC,由于 ∠BOH= α,∠EOH = β,因此∠BOE = β - α,刀尖圓弧與兩段椎體零件分別相切于 B、E 兩點,由幾何 關 系 可 知 EL = BL,因 此 ∠BOL =∠EOL = ( β - α) /2。在∠BOL 中有 BL = rtg[( β - α) /2],在∠BCL中有 LC = BLcosα = rcosαtg[( β - α) /2],此時車刀刀具的實際軸向位移尺寸為 a1= b1- △a1= b1- rcosαtg [( β - α) /2 ],其中
α、β分別表示第一段和第二段椎體的斜度,同時也可以直接得出第二段椎體零件的軸向尺寸變化大小△a2= EG = rcosβtg[( β - α) /2 ],零件的實際軸向位移尺寸 a
2= b2- △a2= b2- rcosβtg [( β - α) /2]。
此時第一段椎體的最大直徑尺寸為 dmax= d1- △d1= d1-2rsinαtg[( β - α) /2],第二段椎體的小端徑向尺寸變化量 △d2=2LG = 2rsinβtg[( β - α /2 ],第二段椎體的最小直徑為 dmin= d2+△d2= d2+ 2rsinβtg[( β - α) /2]。
由以上分析可知,在加工雙段外椎體零件的過程中,受到刀尖圓弧尺寸的變化,零件的軸向尺寸也會出現變化,刀尖圓弧半徑增大的同時,零件軸向尺寸增大,軸向尺寸的變化會受到兩椎體錐角的差值影響,兩椎體錐角增大時軸向尺寸也會增大。分析徑向尺寸的過程中發現,刀尖圓弧增大時,第一段椎體大端的徑向尺寸減小,第二段椎體小端徑向尺寸增大,兩椎體錐角差值增大時,第一段椎體大端的徑向尺寸減小,第二段椎體小端徑向尺寸增大。4 刀尖圓弧半徑影響球面類零件表面加工尺寸加工過程中,車刀和被加工零件的相對位置如圖 4 所示。
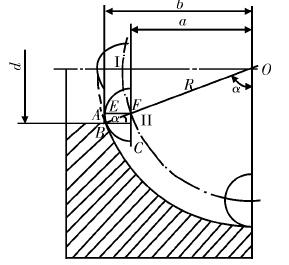
圖 4 球面類零件加工示意
如果加工過程中由內向外走刀,刀具處于位置Ⅰ時,此時零件的軸向尺寸變化為△a = b - a = r,在將非整半球面時,刀具處于位置Ⅱ,此時刀尖圓弧 B 點與球面類零件相切,這種情況下零件的軸線尺寸變化量為△a = b - a = EF = rsinα,其中 α 表示刀具和球面類零件的夾角,此時刀具的實際軸向位移尺寸可以表示為 a = b -△a =
( R - r) sinα,在加工外球面的過程中△a 取負值。
球面零件加工過程中,刀具圓弧 BC 上的不同點依次進行切削,零件的軸向尺寸變化量為△a = EF,球面加工結束后進行大端評價加工時,刀尖圓弧頂點和零件的端面相切,零件的軸向尺寸變為 EF + AE,此時的徑向尺寸變化量△d = 2BE = 2rcosα,此時球面的最大直徑變為 Dmax= D - △d = D - 2rcosα,零件的軸向尺寸由原來的 b 變為b' = b - AE。由以上分析可知,加工內球面零件的過程中,刀尖圓弧半徑影響零件的軸向尺寸變化,刀尖圓弧半徑增大的同時,軸向尺寸減小,球面夾角增大時,軸向尺寸也會減小。
5 、結語
車刀刀具刀尖圓弧半徑影響零件的加工精度,在不同形狀零件的加工過程中,需要重視對零件加工精度的控制。例如在軟件編程過程轉給你可以對刀具刀尖的軌跡進行調整,保證刀尖的實際加工軌跡和理想軌跡相符合,可以借助幾何計算的方法將刀尖軌跡轉換為理想刀尖軌跡,編程過程中嚴格遵守草圖繪制、軌跡模擬、編程的步驟。
另外在實際加工過程中需要及時檢查所應用刀具的圓弧半徑 r,對刀過程中充分考慮刀具刀尖圓弧半徑的影響,可以借助數控車床系統刀具補償功能進行尺寸優化。
投稿箱:
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com





