錯齒內排屑刀具深孔加工中的刀具振動特性對孔圓度形貌的作用機制
2018-4-23 來源:西安理工大學 機械與精密儀器工程學院 作者:孔令飛,牛晗,侯曉麗,林宏斌,王杰
摘要: 依據錯齒內排屑刀具深孔加工的實際特點,構建了受刀具橫向振動特性影響的加工孔圓度形貌模型。運用動力學半解析法,在保證刀具系統動態分析精度的前提下,將復雜深孔刀具系統離散為多段具有局部特征的梁單元,其中相鄰單元之間滿足模態形函數傳遞矩陣的連續條件。結合 Newton-Raphson 迭代法,給出了深孔圓度形貌形成軌跡的數學描述,以及深孔刀具動態特性與加工孔圓度形貌之間的關聯關系。通過數值算例驗證了所提出方法的可行性,同時為實現深孔切削過程加工孔圓度誤差的預測與控制奠定了基礎。
關鍵詞: 機械制造工藝與設備; 深孔鉆削; 刀具振動; 圓度形貌; 半解析法
0、引言
精密高效的錯齒內排屑刀具( BTA) 深孔鉆削技術是當今兵器工業、新能源裝備制造和高新技術產業對深孔零件加工提出的迫切需要。然而,由于深孔鉆削機理的復雜性,實際加工中刀具系統需要承受切削力波動及刀具回轉慣性等的影響,而這些載荷又隨著加工參數的變化而變化,致使刀具所表現出的動態行為極其復雜,進而對加工孔品質產生極大影響。那么,如何構建更加精確的深孔刀具系統動態模型,探明加工參數與加工孔精度的映射關系,實現高效、準確地預測與控制加工孔品質,就成為深孔鉆削研究的熱點和關鍵問題。
Mehrabadi 等構建了考慮鉆削過程阻尼和質量偏心影響的刀具系統動力學模型,討論了刀具動態運行軌跡及其相應的孔圓度形貌特征,并結合實驗證實了該模型的準確性。Bayly 等依據鉆削加工過程的實際特點,研究了顫振對鉆削刀刃切削力和 碰 摩 力 的 影 響,分析了葉瓣孔的成形機理。在此基礎上,Deng 等運用 Euler-Ber-noulli 梁單元模型,并結合深孔切削力的傅里葉函數形式表達式,給出了深孔加工圓度誤差計算模型,進而對波紋型與葉瓣型深孔的形成機理進行了研究。但是,由于刀具系統結構的復雜性,這些將切削力簡化為一階徑向波動分量形式,或是將刀桿簡化為簡支梁模型,以期得到加工孔圓度形貌的數值解或解析解,就不可避免地丟失刀具系統的一些動力學特性。在實際的深孔加工刀具系統中,刀具經常是由多個部件組成的連續體,且包含有多段刀桿及特殊構造的刀頭,因而難以用簡單模型來描述,必須構建更加精確的深孔加工刀具系統模型。
針對上述問題,本文將復雜深孔刀具系統離散為多段具有局部結構特征的梁單元,而相鄰單元之間滿足模態形函數傳遞矩陣的連續條件。然后,利用 Newton-Raphson 迭代法,并結合 BTA 深孔鉆削力的傅里葉多階諧波形式,給出了深孔圓度形貌形成軌跡的解析形式。據此,研究了深孔刀具動態特性與加工孔圓度形貌之間的關聯關系,以及在深孔低速切削過程中易出現葉瓣孔型的成因及其機理。數值算例驗證了本文所提出方法的可行性,該方法將為實現深孔切削過程加工孔誤差的預測與控制奠定基礎.
1、BTA 深孔鉆削系統的動態方程
1. 1 BTA 深孔鉆削系統的模型
深孔鉆削加工是將特殊構型的切削刀具裝在圓形空心鉆桿上,使得工件相對于刀具作高速旋轉運動( 或刀具相對于工件作高速旋轉運動) 。通過授油裝置將高壓切削液沿著鉆桿與孔壁之間的縫隙噴入切削區域,利用切削液自身壓力實現刀具切削部分排屑、冷卻和潤滑。圖1為鉆桿系統示意圖。

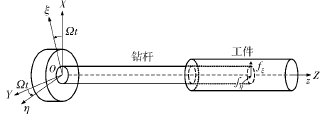
圖1 深孔鉆削刀具系統示意圖
采用 Lagrangian 變分原理,如圖 1 所示的深孔刀具系統應滿足:

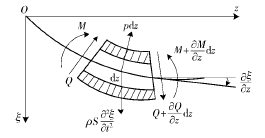
圖2 BTA 鉆桿微分單元
由圖2可以得到 BTA 旋轉鉆桿系統的動能表達式為


1. 2 BTA 深孔加工刀具的動態切削力求解( 6) 式的刀具動態軌跡時,迭代過程需要主切削刃上的切削力、導向塊上的正壓力及摩擦力矢量的多次求和,而矢量力疊加的協調精度不僅影響到求解刀具動態響應是否收斂,而且對被加工孔圓度誤差預測及其演變規律的定量分析具有重要影響。為了方便計算各切削分力的矢量和,可將旋轉坐標系下所描述的刀具受力系統轉化到直角坐標系,如圖 3 所示。圖 3 中: A 表示 BTA 深孔加工刀頭的主切削刃,B、C 表示其兩個導向塊; fAξ、fBξ和 fCξ分別表示切削刃 A、導向條 B 及導向條C在動坐標系ξ方向上的受力,而 fAη、fBη和 fCη分別表示切削刃 A導向條 B 及導向條 C 在動坐標系 η 方向上的受力; θ為刀具旋轉角度,θ = Ωt; αB和 αC分別為切削刃與導向條 B 和 C 的夾角。因此,實際深孔鉆削中,t時刻加工刀具在 X、Y 方向上所承受的矢量疊加力可表示為
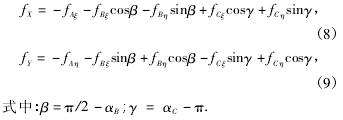
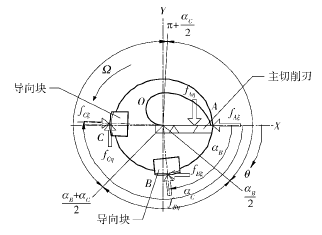
圖3 BTA 深孔加工切削力分布
由圖2可以得到 BTA 旋轉鉆桿系統的動能表達式為

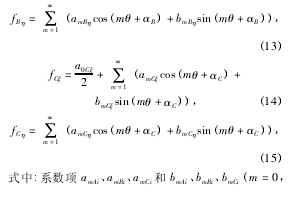

2 、深孔圓度形貌的形成軌跡

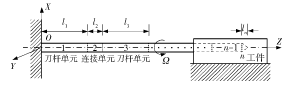
圖4 深孔鉆削刀具系統模型
圖4中,經離散化處理后的深孔刀具系統可分為 n 個結構單元,其中第 i 段梁的模態函數為


采用與( 20) 式相似的推導過程,若取 i = 1,2,…,n 時,則自由邊界條件下 BTA 深孔刀具系統模態形函數的傳遞矩陣可寫為(21)式的形式。Deng 等和 Hussien 等的研究結果表明深孔刀具系統的邊界條件可假設為簡支梁,且具有足夠的精度。因此,根據(22) 式的刀具單元模態傳遞形式,并綜合考慮邊界條件,便可得刀具系統的連續傳遞函數(22) 式。



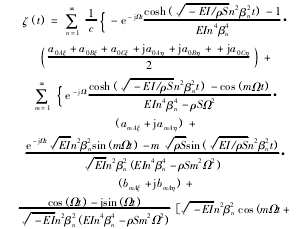
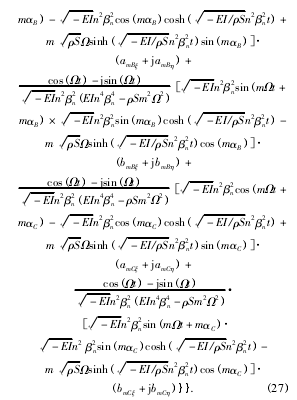
就(27) 式的本質而言,被加工孔的動態形貌軌跡 ζ( t) 是深孔刀具振動過程中 n 階振動模態函數的疊加。利用( 27) 式,并結合 Shunmugam 提出的最小二乘圓法,即可很容易地獲得被加工孔的圓度誤差。
3 、方法驗證
為了驗證方法的可行性,運用上述理論和算法編制程序,將計算結果與文獻的實驗結果進行對比。相關計 算參數如下: 鉆桿材料密度為7860 kg / m3,彈性模量為 2.06×1011Pa; 刀具直徑分別選用 18. 91 mm 和 26. 40 mm 兩種,其中刀具直徑為 18. 91 mm 時,鉆桿的內徑與外徑分別為11. 5 mm和 17 mm,而當刀具直徑為 26. 40 mm 時,鉆桿的內徑與外徑分別為 14 mm 和 22 mm.
表1 為在不同切削轉速、進給量及加工深度條件下,計算得到的被加工孔圓度誤差數值。由表 1可以看出,當選定加工深度時,若改變鉆削進給量、切削轉速或鉆桿直徑參數,被加工孔圓度誤差的預測結果與實驗結果的變化趨勢是相同的,即隨著鉆削進給量的增加、切削轉速的增大及鉆桿直徑的減少,被加工孔的圓度誤差均在不同程度上增大。例如當選定加工深度為 150 mm 時,鉆削進給量從0.05 mm / r 增加到 0. 1 mm / r,圓度誤差的預測結果從 2. 9 μm 增加到 4. 9 μm,而實驗結果則從 2. 7 μm增加到 4. 8 μm; 若選定加工深度為 200 mm 時,切削轉速從 390 r/min 增加855 r/min,圓度誤差的預測結果與實驗結果分別從 2. 8 μm 增加到 4. 9 μm 和從 2. 6 μm 增加到 5. 2 μm. 此外,盡管孔圓度誤差的預測結果與實驗結果存在一些差異,但二者之間的誤差幾乎都在 10% 以內,這表明本文所提出的方法適用于預測被加工孔的圓度誤差及其變化趨勢,且具有較高的精度。然而,就預測結果與實驗結果之間的差異而言,主要是由于本文采用的切削力模型尚存在不足之處,例如導向塊與孔壁表面之間的摩擦效應、材料本身的性能等因素未被考慮。

表1 圓度誤差的理論計算與實驗結果對比
4 、應用算例與分析
本節將運用前文所述的算法編制程序,探究不同切削轉速條件下,刀具中心動態軌跡與孔表面圓度形貌之間的關聯聯系,進而為實際加工過程中精準預測或控制被加工孔的圓度誤差奠定基礎。圖5~圖 7 分別給出了當進給量為 0. 1 mm/r、鉆桿長度為 1. 6 m 及刀具直徑為 18. 91 mm 時,選取390 r / min、560 r / min 和 830 r / min 3 種不同切削轉速進行加工,獲得的刀具中心動態軌跡。從圖5~圖7中可以看出,隨著切削轉速的增大,刀具中心動態軌跡的振動范圍不斷增大,但振動特征卻呈現出明顯差異。例如當刀具轉速為 390 r/min 時,刀具中心的動態軌跡呈現出明顯的 4 波瓣軌跡,而切削轉速為560 r / min 和 830 r / min 時,上述現象卻并不明顯。為了進一步研究孔圓度形貌的形成機制,可取上述相同的加工參數,繪制出孔圓度形貌軌跡,如圖8所示。從圖 8 中可以看出,對于 3 種不同的切削轉速而言,刀具每切削一個周期所形成的圓度形貌軌跡與相鄰兩周之間均存在著一個相位差εp,進而造成了相鄰切削周期內所形成的孔型存在角度差異。若相位差εp越小,則相鄰切削周期的孔型偏差也就越小。結合 Bayly 等和 Tlusty的研究可知,孔圓度形貌的偏差與刀具系統固有特性有著直接聯系。基于此,利用本文所述的數值計算方法,獲得深孔刀具系統的第 1 階固有頻率為 25. 2 Hz,將其轉化成相應的轉速單位為 1 510. 8 r/min. 若選取切削轉速為 390 r/min 時,該值恰好接近于固有頻率的四分之一( 即 377. 7 r/min) ,因而被加工孔圓度形貌呈現出明顯的 4 瓣特征,如圖 8 ( a) 所示。圖9 ~圖 12給出了當切削轉速分別為深孔鉆桿系統第 1 階固有頻率的 1 /2、1 /3、1 /4 和 1 /5 時,計算獲得的刀具中心動態軌跡,相應的波瓣數為 2 瓣、3 瓣、4 瓣、5 瓣。通過上述數值算例可以看出,雖然實際鉆削中引發孔圓度形貌變化的原因不同,但其形成的過程和出現的規律是相同的,即孔圓度形貌與刀具系統的低階固有頻率及激勵頻率有著最為直接的聯系。
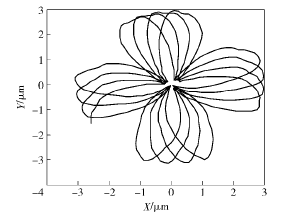
圖5 當 Ω = 390 r/min 時刀具中心的動態軌跡

圖6 當 Ω = 560 r/min 時刀具中心的動態軌跡
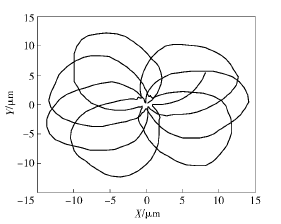
圖7 當 Ω = 830 r/min 時刀具中心的動態軌跡
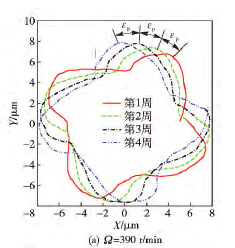

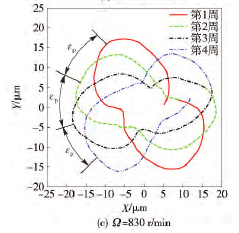
圖8 不同轉速時孔表面圓度的二維形貌軌跡
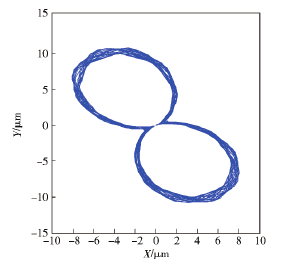
圖9 當 Ω = 755. 4 r/min 時刀具中心的動態軌跡
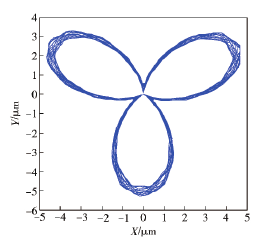
圖10 當 Ω = 503. 6 r/min 時刀具中心的動態軌跡
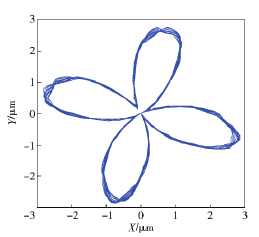
圖11 當 Ω = 377. 7 r/min 時刀具中心的動態軌跡
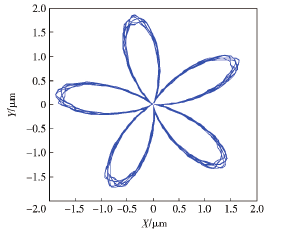
圖12 當 Ω = 302. 16 r/min 時刀具中心的動態軌跡
5 、結論
考慮到實際深孔加工刀具系統結構的復雜性,將刀具系統離散為多段具有局部結構特征的梁單元,其中相鄰單元之間滿足模態形函數傳遞矩陣的連續條件,進而構建了深孔圓度形貌形成軌跡的解析表達式。運用該數值計算方法,研究了刀具動態特性與加工孔圓度形貌之間的關聯關系。由數值計算結果可以看出,雖然深孔鉆削過程中引發孔圓度誤差變化的原因不同,但其形成的過程和出現的規律是相同的,即孔圓度誤差形貌與刀具系統的固有頻率及激勵頻率有著最為直接的聯系。此外,算例結果也驗證了本文所提出的方法適用于探究被加工深孔圓度誤差的變化規律,這些將為實現深孔切削過程加工孔圓度誤差的預測與控制奠定基礎,且具有足夠的精度。
投稿箱:
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
更多相關信息




