摘要:為了更好地實現螺旋錐齒輪精密數控加工,結合螺旋錐齒輪加工特點,在歐式線性空間中建立了數控加工模型及誤差補償模型。補償模型為二級補償機制,以齒面誤差作為判斷依據,通過對機床安裝調整誤差的補償和加工過程中運動誤差的補償及時修正加工質量。由此,通過逐齒動態補償,使得加工過程中機床誤差得到修正,齒面加工精度得到提升。經仿真實驗驗證,該方法可實現連續軌跡運動中的多軸協調,有效提高螺旋錐齒輪數控加工機床的加工精度。
0 引言
螺旋錐齒輪是空間自由曲面,需要五軸、六軸聯動加工,加工誤差具有實時變化的隨機性且對齒面不同部位誤差的影響也有大小和正負之分 。理論齒面上任意一點的齒面誤差可以認為是機床各軸微小變化引起的齒面誤差的疊加 。
在車間中,通常采用離線誤差測量而后依據經驗手動調整的方法對初始齒坯安裝和機床定位參數進行定性修正。隨著數字化制造理論與技術的發展,齒面誤差補償研究多集中在初始安裝參數對接觸區形狀位置的影響分析上 。
但在實際加工過程中,不確定影響因素所引起的實時加工路徑變化對齒面精度存在很大影響。可是,受機床結構的影響,在螺旋錐齒輪加工機床上建立實時補償系統很困難。例如,五軸或六軸耦合運動增加了反饋補償算法的復雜度;加工空間小妨礙了實時監測設備的安裝調試。
為此,本文采用機床精度設計和運動學標定兩種途徑對齒輪產品精度進行初步估算,在已有安裝誤差補償基礎上建立一種可實時監控反饋調整的機床控制策略,以提高系統動態特性,增強各軸間運動協調與參數匹配能力,實現螺旋錐齒輪精密數控加工。
1 基于集合理論的精度分析方法
定義1 集合A 為映射f 的定義域,記為D(f)。


使用基于集合理論的精度分析方法,可將螺旋錐齒輪精密數控加工誤差補償方法描述為:建立對加工過程誤差的補償策略,以縮小定義域A的波動范圍,經過函數f映射,得到最小的產品質量波動空間B。定義域的波動空間由兩部分誤差造成:一部分為安裝調試過程各軸的安裝誤差,另一部分為動態加工過程中各軸的重復定位誤差。
2 螺旋錐齒輪數控加工模型
本文選取國產YK2275數控銑齒機(圖1)為對象,以格里森齒制螺旋錐齒輪滾切法數控加工大輪為例,進行具體研究。數控加工的基本原理就是保證切齒過程中刀軸(或砂輪軸)與工件軸在任一瞬時的相對位置與傳統加工時相同,運動關系相同。
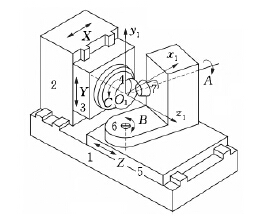
圖1 YK2275數控銑齒機
1.床身 2.X 軸工作臺 3. Y 軸工作臺 4.刀盤5.Z 軸工作臺 6.工件主軸 7.工件
2.1 含誤差的齒面模型
基于多體系統理論描述機床拓撲結構,為其各部分編號,如圖1所示。令大地編號為0,將銑齒機系統分為兩個分支:① 床身、X 軸工作臺、Y 軸工作臺、刀盤,銑齒刀;② 床身、Z 軸工作臺、工件主軸、工件。




依據YK2275型螺旋錐齒輪銑齒機各個部件之間的運動關系,建立包含機床幾何誤差的相鄰體變換矩陣如下。
(1)刀盤與Y 軸工作臺之間變換矩陣為

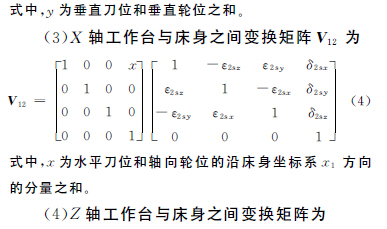


(6)A 軸工作臺與B 軸工作臺之間變換矩陣為



2.2 齒面離散
在工程實際測量中,通常沿齒寬方向取9排齒面點,每排取5個數據點,在齒面上均勻地取45個點,建立全齒面的離散曲面[8?9],如圖2所示。本文的齒面離散方法正是基于這種思想,以已建立的齒面模型為基礎,在齒面上選取m×n個網格點作為數字化齒面。具體做法為:將理論齒面向過齒輪軸線的某一平面旋轉投影,形成拓撲平面;在該
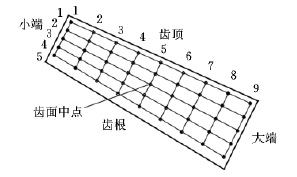
圖2 離散齒面
拓撲平面上取齒寬和齒高方向分別為X 軸和Y軸,其上任一點對應齒面點的法向誤差值為該點的Z坐標值,形成新曲面。新曲面上點的位置按照下式進行計算:

2.3 映射函數推導
各軸誤差依據拉丁超立方抽樣法[10] 進行模擬,抽樣區間為[-0.01,0.01],平移量單位為mm,旋轉量單位為(°)。每項誤差擬合樣本數為10,且在區間內均勻分布。抽樣過程可分為單軸誤差影響分析和綜合誤差分析兩步進行。各軸位置誤差與運動誤差對齒面誤差的映射關系記為影響系數MG:


依據擬合樣本計算齒面各點齒形偏差,選用一階、二階或更高階次回歸方程進行數據擬合 。經過擬合結果分析對比,一階模型預測效果較差,三階模型預測誤差比二階模型稍大。所以,本文選用二階模型公式
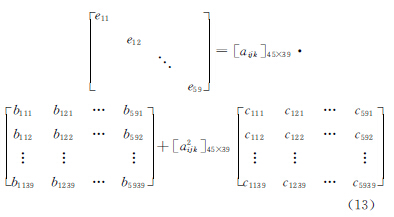
作為映射函數,描述幾何誤差綜合作用對齒形造成的影響。
2.4 誤差補償算法
在大輪加工過程中,X軸、Y 軸、Z軸的運動始終描述刀盤原點相對于工件原點的位置矢量。B軸保持固定角度,保證切削出根錐角。A 軸按照搖臺滾輪的滾比關系做輪坯回轉運動,此外,在一個齒加工完成后,做分度運動。數控加工模型如下:
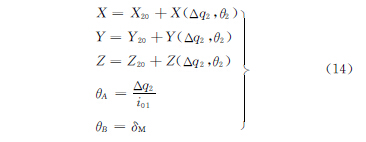
其中,X軸、Y 軸、Z軸運動的第一項均為機床基本參數調整的常數項,與機床結構與被加工齒輪具



誤差,分析整理出齒面誤差變化曲線圖。隨后,將誤差變化曲線作為補償模型輸入,計算數控機構中X、Y、Z、A、B 軸動態運動修正值,并將其作為補償模型的輸出,實現對整個加工過程中齒面誤差的補償。
圖3為控制系統結構框圖。
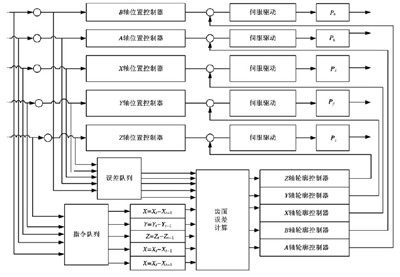

3 仿真實驗與結果分析

輪的動態加工過程。參照表1中齒輪副幾何參數、機床調整參數,建立的理論齒面如圖4a所示,采用離散齒面的形式;隨機選取第5齒作為研究對象,由不同機床幾
何誤差生成不同的誤差齒面,如圖4b~圖4d所示,分別為Y 軸直線運動誤差引起的誤差齒面、A軸回轉運動誤差引起的誤差齒面以及B 軸定位誤差引起的誤差齒面。
表1 齒輪幾何參數與機床調整參數
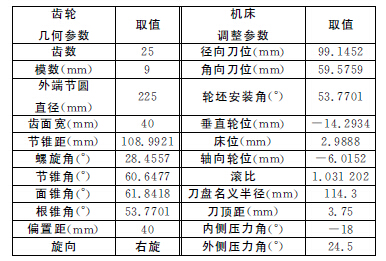
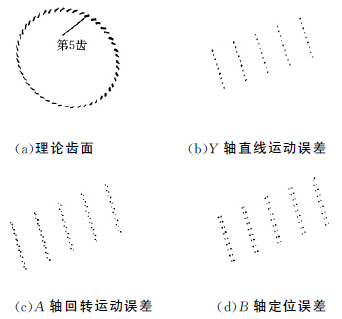
圖4 理論齒面與誤差齒面
依據國家標準GB/T11365-89,選取單周節偏差描述齒面加工精度。如圖5所示,其定義為分度圓上,實際齒廓上一點的位置與相鄰齒同側齒廓點的位置之間的距離與理論值間的距離的差。計算公式如下:
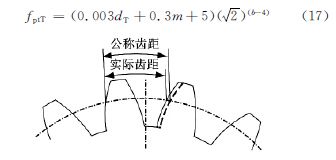
圖5 齒形偏差定義
式中,dT為公差直徑,即中點錐距處與工作齒高中點相交處的直徑;m 為中點法向模數,即在中點錐距處法平面上節圓直徑與齒數的比值;b為精度等級。
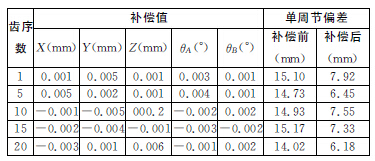
表2顯示了實時補償值與補償后的齒面單周節偏差。按照式(17)計算可知,補償前,齒面精度為6級,補償后齒面精度達到4級。仿真結果證明,采用螺旋錐齒輪加工誤差補償策略,可以明顯提高螺旋錐齒輪五軸聯動數控系統的加工精度。
表2 機床參數動態調整示例
4 結論
(1)依據機床精度與齒面加工質量間的映射關系數學模型,建立兩級數控加工誤差補償模型,對加工過程不確定因素對齒面造成的加工質量誤差進行了有益補償,實現了齒面輪廓補償控制,提高了齒面各點位置精度,能夠使產品更好地滿足齒輪設計精度要求。
(2)利用非線性最小二乘優化方法求解齒面上各點誤差最小以及該時刻機床各軸運動修正量最優解。該方法能夠準確有效地將齒面誤差補償分解到各軸運動補償中。
(3)為提高模型的準確性,可重復加工過程,對加工出的齒輪齒面誤差進行統計分析計算,建立誤差范圍與修正值的關系。另外,將建立運動軸變化與齒面接觸區變化的關系模型,實現對接觸區的動態修正。
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com




