數控磨床主軸系統的可靠性建模與評估研究
2021-2-1 來源:北京工業大學機械工程與應用電子技術學院等 作者:范晉偉,薛良良,劉 強,李偉華
摘 要: 對北京第二機床廠某系列數控磨床主軸系統的故障數據進行處理,繪制主軸系統的概率密度函數散點圖,初步假定函數模型,再利用最小二乘法估計未知參數,利用卡方檢驗和相關系數法進行擬合優度檢驗,最終確定主軸系統的分布類型為指數分布。根據所屬分布類型計算主軸系統的平均故障間隔時間 MTBF,平均維修時間 MTTR,以及固有可用度 A,對主軸系統的可靠性進行評估。所得結果已反饋到生產廠家并獲得認可,對數控磨床整機可靠性的提升有重要意義。
關鍵詞: 主軸系統; 可靠性建模; 數據擬合; 可靠性評估
主軸系統是數控磨床的關鍵組成系統,其可靠性的高低直接影響產品加工的質量和效率。如何提高主軸對整機的可靠性是急需解決的問題。目前國內外學者對主軸系統可靠性的研究主要分為以下 5 個方面:( 1) 故 障 樹 分 析 ( FTA) 。羅 靜 等 結 合 層 次 分 析 法( AHP) 對主軸建立了故障遞階層次模型,確定了影響主軸 系統的關鍵故 障因 素,提高了主 軸 系 統 可 靠性; 張英芝等運用模糊故障樹理論,對數控車床主軸系統進行了故障樹定量分析。( 2) 故障模式影響及危害性分析( FMECA) 。王德超等對 161 臺加工中心主軸進行了 FMECA 分析,采用模糊評判法計算了危害度,并擬合模型計算了首次故障間隔時間; 王廣勇等對數控銑床主軸系統進行了 FMECA 分析,并對故障原因提出了改進措施。( 3) 熱特性分析。佟威等借助于 ANSYS 的 Workbench 平臺,研究了主軸溫度場、應力和變形分布規律; 樓婷婷等對立式加工中心主軸可靠性虛擬樣機建模理論進行了深入研究,完成可靠性虛擬樣機的建立,并分析了熱特性對其可靠性的影響; Ali Zahedi 等提出了一個包括其主要部件的機械和熱行為的高速主軸可行模型。( 4) 振動分析。張義民等利用一次二階矩法計算了主軸系統在特定轉速下的可靠度; 張愛華等運用 ANSYS 軟件中參數化設計語言與蒙特卡羅法相結合的隨機有限元法研究了高速電主軸抗共振的可靠性,并通過 PDS模塊計算出了高速電主軸抗共振的可靠度; JiangDayong 等通過對主軸振動特性的提取,提出了一種利用比例風險模型將振動特征等低層信息與可靠性指標等高層信息連接起來的新方法。( 5) 主軸軸承可靠性分析。沈延軍等基于多狀態理論對軸承進行可靠度分析,運用通用生成函數法得到軸承可靠度。Young-Kug Hwang 等研究了軸承的預緊力對主軸運行的影響,詳細介紹了預加載技術并運用到了主軸系統上;Vincent Gagnol 等提出了一種基于有限元模型分析和實驗模態識別相結合的高速主軸軸承系統建模方法。
表1:主軸系統故障記錄表

通過查閱相關文獻發現,當前的研究側重于熱態特性、軸承以及動態性能模塊,對于主軸系統建立故障時間模型的研究相對較少,模型建立的過程也相對簡單,沒有對故障數據進行細化處理。因此本文將從數控磨床主軸系統的故障數據采集,故障數據處理,可靠性模型建立,模型參數估計、假設檢驗、模型優選以及可靠性評估等方面對主軸系統進行全面的分析和研究,最終確定磨床主軸系統的數學模型,算出平均故障間隔時間,為廠家提高數控磨床整機的可靠性提供技術支持。
1、可靠性建模
根據《數控機床可靠性評定》總則,采取定時結尾試驗的方法現場跟蹤磨床的運行情況。在采集故障數據時,嚴格遵循總則中故障的 4 條判定原則和 3條故障計數原則,正確記錄故障發生時間、故障部位,故障現象,采取措施和維修時間。本文的可靠性數據均來自北京第二機床廠同一型號磨床現場試驗數據以及廠家用戶故障反饋信息。其中記錄關于主軸系統的故障數據為 62 條。表1為部分故障數據。
從故障記錄表中簡單分析可以得出,主軸系統故障主要包括主軸軸承和電機軸承的損壞,皮帶斷裂,皮帶磨損和打滑,占總故障的 60%左右,皮帶和軸承是主軸系統故障的主要原因。由于主軸是磨床廠家生產制造,為此在設計制造時應作出改進。下面對其故障間隔時間模型做詳細分析。
2.1、故障數據處理及散點圖繪制
將可靠性數據按時間進行分組,分組數量太大或太小,都會使得每個區間的故障數量極端化,增加擬合誤差。組數 K 的大小通常按經驗公式來確定,如式( 1) 所示:
式中: nf為系統的故障數據總數; K 為分組的數量,經計算取整為 7。
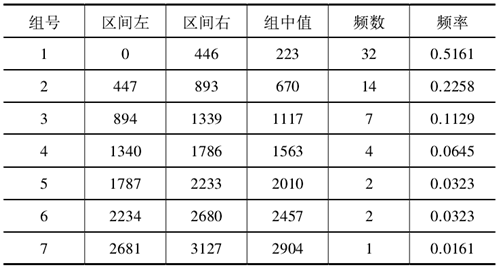
求出每個區間的故障數量以后,用式( 2) 可以求出每個區間內故障概率密度的觀測值,如表2所示。
表2:故障間隔時間分組表
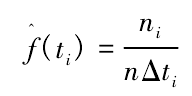
式中: ti為每組故障數據區間中值; n 為故障總數; ni為每組故障頻數,Δti為區間長度。
表3:故障概率密度和累積概率表
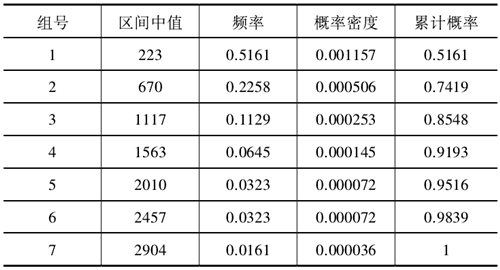
由表3可得到主軸系統的概率密度散點圖,如圖1 所示,從圖中可以看出,該系列數控磨床主軸系統的故障概率密度呈單調遞減的趨勢,可以近似認為符合指數分布和威布爾分布模型。
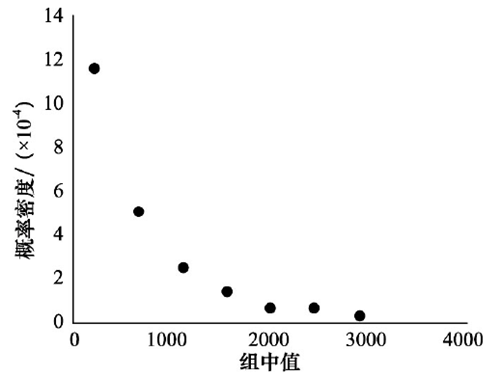
圖1:概率密度函數散點圖
2.2、參數估計
在初步確定了故障分布類型以后,需要對故障概率密度函數進行參數估計。最小二乘法因為簡單易行是常用的方法之一。下面對指數分布和威布爾分布分別用最小二乘法進行參數估計。
( 1) 指數分布模型
指數分布的概率密度函數和累積分布函數分別為:
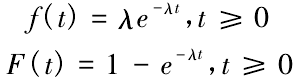
式中: λ 是失效率,為未知參數。
將( 4) 式取對數變換,得到:
令 y = 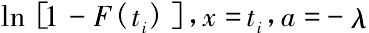 則可以得到y =ax,
則可以得到y =ax,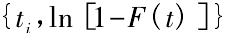 是滿足線性關系的。最小二乘法公式為 y =ax+b,其參數估計量為:
是滿足線性關系的。最小二乘法公式為 y =ax+b,其參數估計量為:
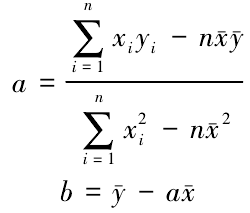
式中: 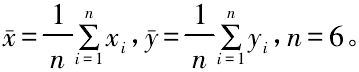
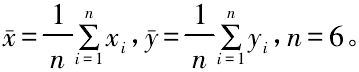
代入表 2 故障數據進行整理,計算可得:
a = -0.00145
因此指數分布線性表達式為:
y = -0.00145x
繪制( x,y) 散點圖,擬合一元線性函數,如圖 2 所示。經初步判斷,主軸系統故障間隔時間指數分布模型有效合理。
若故障間隔時間數據符合指數分布,則由上述分析可得到指數分布的參數 λ = 0.001 45,累積分布函數為 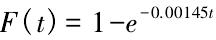 。
。
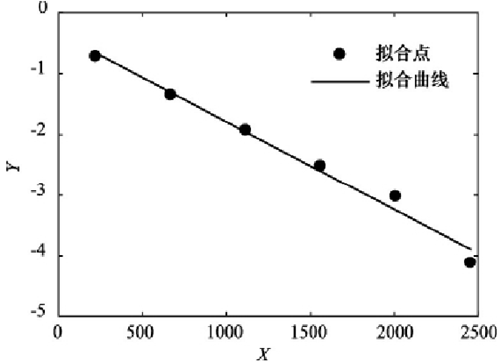
圖2:指數分布擬合圖
( 2) 威布爾分布模型
二參數威布爾分布的累計分布函數為式( 9) 所示,有 η 和 β 兩個未知參數。為方便進行一元線性回歸,將式( 9) 進行兩次對數變換,結果為式( 10) 。
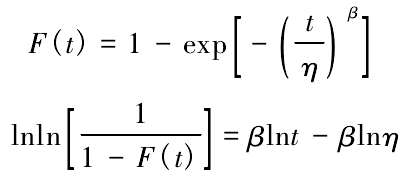
令 y =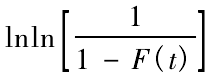 ,x = lnt ,若故障間隔時間符合威布爾分布,則 y 和 x 滿足線性關系 y = βx -βlnη。 通過最小二乘法參數計算公式( 6) 和( 7) ,即可求得回歸方程 y = ax + b 中的回歸系數 a 和 b,進而確定未知參數與回歸系數的關系如下所示:
,x = lnt ,若故障間隔時間符合威布爾分布,則 y 和 x 滿足線性關系 y = βx -βlnη。 通過最小二乘法參數計算公式( 6) 和( 7) ,即可求得回歸方程 y = ax + b 中的回歸系數 a 和 b,進而確定未知參數與回歸系數的關系如下所示:
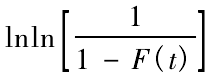 ,x = lnt ,若故障間隔時間符合威布爾分布,則 y 和 x 滿足線性關系 y = βx -βlnη。 通過最小二乘法參數計算公式( 6) 和( 7) ,即可求得回歸方程 y = ax + b 中的回歸系數 a 和 b,進而確定未知參數與回歸系數的關系如下所示:
,x = lnt ,若故障間隔時間符合威布爾分布,則 y 和 x 滿足線性關系 y = βx -βlnη。 通過最小二乘法參數計算公式( 6) 和( 7) ,即可求得回歸方程 y = ax + b 中的回歸系數 a 和 b,進而確定未知參數與回歸系數的關系如下所示: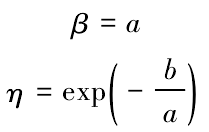
將表 3 故障間隔時間數據代入計算得 a = 0.696,b= -4.155。因此威布爾分布線性表達式為:
y = 0.696x - 4.155
繪制( x,y) 散點圖,同時擬合一元線性函數,如下圖 3 所示。經初步判斷,主軸系統故障間隔時間符合威布爾分布模型。
若故障間隔時間數據符合威布爾分布,則由上述分析可得到威布爾分布的參數為 β = 0.696,η = 391.7。累積分布函數為 F( t) =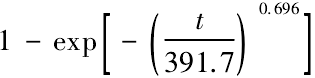 。
。
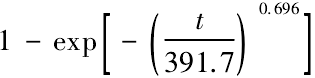 。
。 2.3、擬合檢驗
由上圖 2、圖 3 可以看出指數分布和威布爾分布都近似符合磨床主軸系統的故障時間模型,但是很難得出概率密度觀測值與擬合曲線之間是否真的具有關聯性,或關聯度大小,因此需要對上兩種模型假設進行擬合檢驗。
此次檢驗采用 χ2檢驗,原理是將檢驗統計量 χ2的觀測值與臨界值進行比較,計算理論頻數與實際頻數之間的差異,如果滿足式( 14) 的條件,則接受原定假設,否則拒絕原假設。
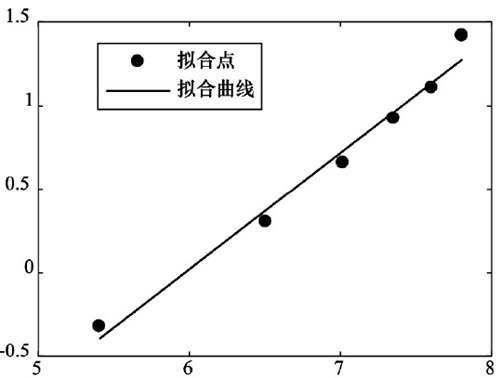
圖3:威布爾分布擬合圖
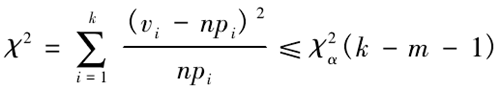
式中: n 為樣本數量 62; k 為分組數量 7; vi為第 i 分組的實際頻數; npi為理論頻數; m 為未知參數,α 為顯著性水平。
( 1) 指數分布模型檢驗
由參數估計可得指數分布的概率密度函數為式( 15) 所示,概率密度函數擬合圖為圖 4 所示:
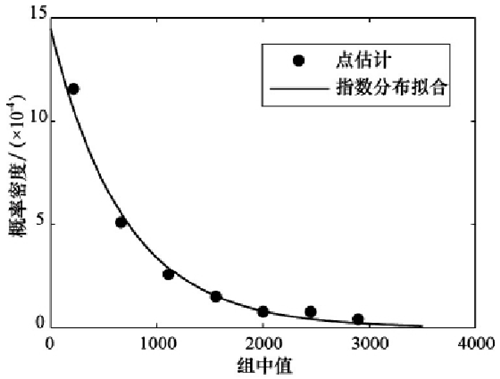
圖4:指數分布概率密度擬合圖
由式 ( 14) 計算出指 數分布時的χ2值 為: χ2e=1.366,在顯著水平 α = 0.05 時,查卡方檢驗臨界值表,在 5 個自由度下的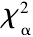 = 11.071。由于
= 11.071。由于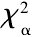 <
<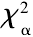 ,所以假設成立,主軸系統故障間隔時間函數符合指數分布。
,所以假設成立,主軸系統故障間隔時間函數符合指數分布。
( 2) 威布爾分布模型檢驗
由參數估計可得威布爾分布的概率密度函數所式( 16) 所示,概率密度函數擬合圖為圖 5 所示:
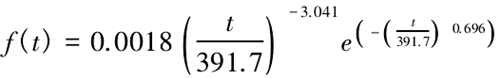
由式( 14) 計算出威布爾分布時的 χ2值為: χ2w=8.498,在顯著水平 α = 0.05 時,查卡方檢驗臨界值表,在 4 個自由度下的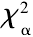 = 9.488。由于
= 9.488。由于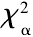 <
<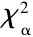 ,所以假設成立,主軸系統故障間隔時間函數符合威布爾分布。
,所以假設成立,主軸系統故障間隔時間函數符合威布爾分布。
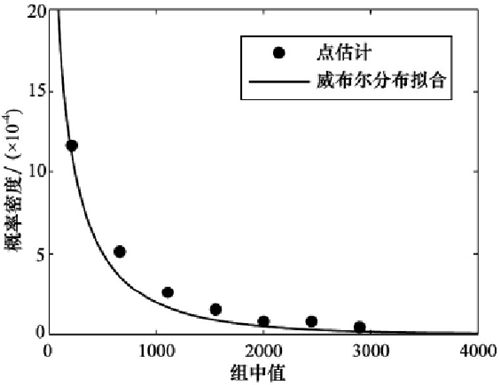
圖5:威布爾分布概率密度擬合圖
2.4、模型優選
通過擬合檢驗,發現指數分布和威布爾分布均符合主軸系統的故障間隔時間模型,從概率密度擬合圖中大致可以看出指數分布模型擬合效果更佳,卡方檢驗中指數分布每組的理論頻數與實際頻數也較為接近。為了準確比較擬合優度,確定最優模型,還需進行線性相關性檢驗。
相關系數法常用于線性回歸檢驗是此次模型優選的方法,用線性相關系數 R 來表示,如式( 17) 所示,R 值越大,表示函數擬合效果越好,線性度也越高。
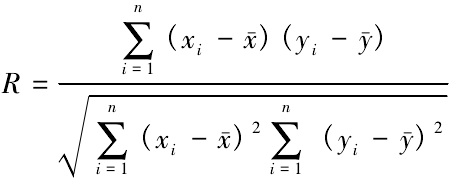
式中: xi為第 i 個樣本數據觀測值,x- 是樣本數據均值,yi是擬合模型第 i 個值,y- 是擬合模型均值。
經計算指數分布的線性相關系數 Re和威布爾分布的線性相關系數 Rw分別為:
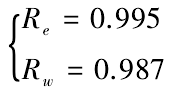
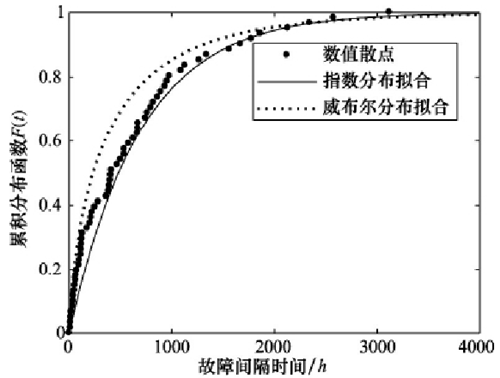
圖6:主軸系統故障間隔時間累積分布擬合圖
指數分布、威布爾分布擬合效果圖如圖 6 所示,且由計算結果可以看出,Re> Rw,指數分布函數擬合效果更優。
3、可靠性評估
通過上述模型分析,主軸系統故障間隔時間服從指數分布,為了從時間值的角度描述其可靠性,本文采用平均故障間隔時間 MTBF,平均修復時間 MTTR,以及固有可用度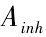 來評估。
來評估。
( 1) 平均故障間隔時間
平均故障間隔時間( MTBF) 是指產品一次故障到下一次故障的平均工作時間,是常用的可靠性評價指標。式子如下所示,f( t) 為概率密度函數。
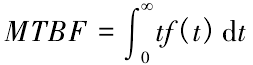
指數分布的概率密度函數為式( 15) ,代入求得主軸系統的平均故障間隔時間為:
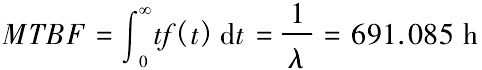
( 2) 平均修復時間
平均修復時間( MTTR) 是產品從發現故障到維修完成、恢復生產所用的時間的平均值。平均修復時間與故障次數和每次故障維修所發生的時間有關,計算公式如下:
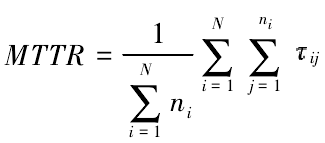
式中: N 為產品總數; ni為第 i 個產品的維修次數; ij為第 i 個產品第 j 次維修所用的時間。
根據得到的故障數據分析,主軸系統的平均維修時間為 MTTR = 1.688 h。
( 3) 固有可用度
產品的固有可用度是產品能正常工作的時間與服務時間的比值,即在規定條件下,
產品保持其功能的概率,計算公式如下:
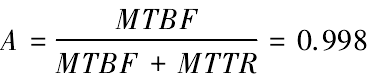
4、結語
通過對機床廠采集的故障數據進行處理分析,對數控磨床主軸系統進行了可靠性建模和評估。首先對數據進行了分組處理,散點圖的繪制,初步假定了主軸系統的故障模型符合指數分布和威布爾分布。然后分別對其進行了參數估計、擬合檢驗、模型優選,最終確定了主軸系統符合指數分布。利用指數分布的函數表達式求出了主軸系統的平均故障間隔時間MTBF=691.085 h,平均維修時間 MTTR = 1.688 h 和固有可用度A= 0.998。以上擬合的模型和計算結果及時反饋給了廠家,并得到了廠家的認可。這為數控磨床其他子系統可靠性建模和評估提供了參考,對整機可靠性分析有重要意義。
投稿箱:
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
更多相關信息




